Question Number 110749 by mnjuly1970 last updated on 30/Aug/20
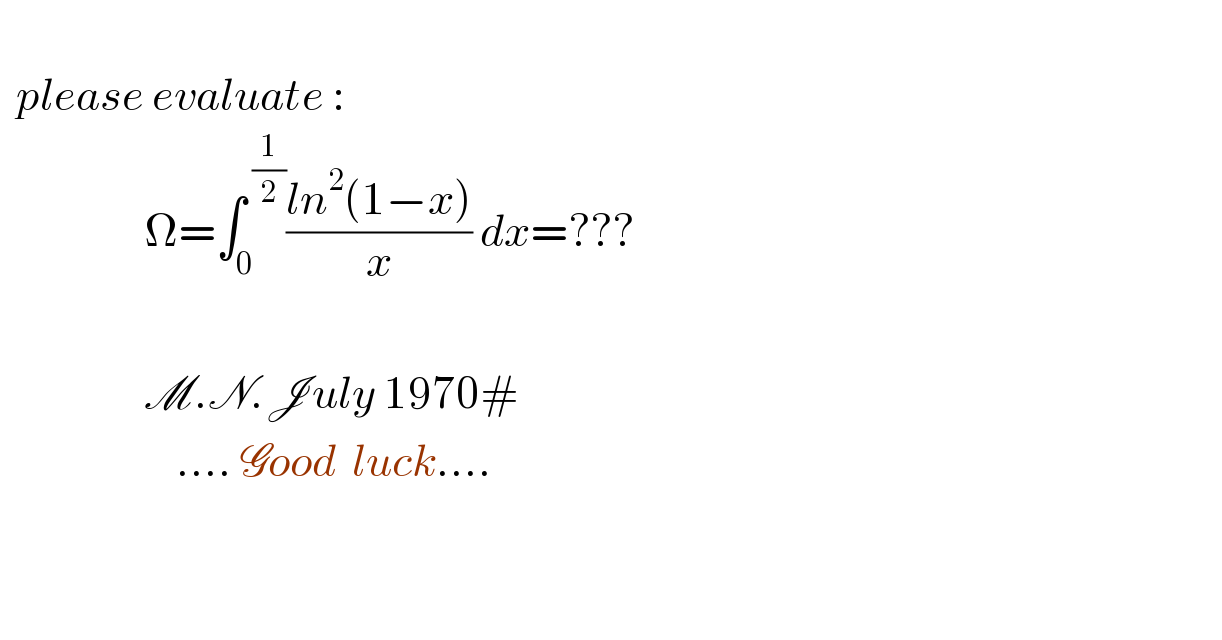
$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:{please}\:{evaluate}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{{x}}\:{dx}=???\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathscr{M}.\mathscr{N}.\mathscr{J}{uly}\:\mathrm{1970}# \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:\mathscr{G}{ood}\:\:{luck}…. \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 30/Aug/20
![Ω =∫_0 ^(1/2) ((ln^2 (1−x))/x)dx ⇒Ω =_(1−x=t) − ∫_1 ^(1/2) ((ln^2 t)/(1−t)) dt =∫_(1/2) ^1 ((ln^2 (t))/(1−t))dt =∫_0 ^1 ((ln^2 (t))/(1−t))dt−∫_0 ^(1/2) ((ln^2 t)/(1−t))dt =I−J I =∫_0 ^1 ((ln^2 t)/(1−t)) dt =∫_0 ^1 ln^2 t Σ_(n=0) ^∞ t^n dt =Σ_(n=0) ^∞ ∫_0 ^1 t^n ln^2 t dt ∫_0 ^1 t^n ln^2 t dt =[(t^(n+1) /(n+1))ln^2 t]_0 ^1 −∫_0 ^1 (t^(n+1) /(n+1))×((2lnt)/t) dt =−(2/(n+1)) ∫_0 ^1 t^n ln(t)dt =−(2/(n+1)){ [(t^(n+1) /(n+1))lnt]_0 ^1 −∫_0 ^1 (t^n /(n+1)) dt} =−(2/(n+1)){−(1/((n+1)^2 ))} =(2/((n+1)^3 )) ⇒I =2 Σ_(n=0) ^∞ (1/((n+1)^3 )) =2ξ(3) J =∫_0 ^(1/2) ((ln^2 t)/(1−t)) dt ? we have J =∫_0 ^(1/2) ln^2 tΣ_(n=0) ^∞ t^n dt =Σ_(n=0) ^∞ ∫_0 ^(1/2) t^n ln^2 t dt but ∫_0 ^(1/2) t^n ln^2 t dt =[(t^(n+1) /(n+1))ln^2 t]_0 ^(1/2) −∫_0 ^(1/2) (t^(n+1) /(n+1))×((2lnt)/t) dt =((ln^2 2)/((n+1)2^(n+1) )) −(2/(n+1)) ∫_0 ^(1/2) t^n ln(t)dt =((ln^2 (2))/((n+1)2^(n+1) ))−(2/(n+1)){ [(t^(n+1) /(n+1))ln(t)]_0 ^(1/2) −∫_0 ^(1/2) (t^n /(n+1))dt} =((ln^2 (2))/((n+1)2^(n+1) ))−(2/((n+1))){((−ln2)/((n+1)2^(n+1) ))−(1/((n+1)^2 2^(n+1) ))} =((ln^2 2)/((n+1)2^(n+1) )) +((2ln2)/((n+1)^2 2^(n+1) ))−(2/((n+1)^3 2^(n+1) )) ⇒ J =ln^2 2Σ_(n=0) ^∞ (1/((n+1)2^(n+1) ))+2ln2 Σ_(n=0) ^∞ (1/((n+1)^2 2^(n+1) ))−2Σ_(n=0) ^∞ (1/((n+1)^3 2^(n+1) )) =ln^2 2Σ_(n=1) ^∞ (1/(n 2^n )) +2ln(2)Σ_(n=1) ^∞ (1/(n^2 2^n )) −2 Σ_(n=1) ^∞ (1/(n^3 2^n )) rest to find the values of those series ...be continued...](https://www.tinkutara.com/question/Q110786.png)
$$\Omega\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:\:\Rightarrow\Omega\:=_{\mathrm{1}−\mathrm{x}=\mathrm{t}} \:\:−\:\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\mathrm{dt} \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}}\mathrm{dt}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}}\mathrm{dt}−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}−\mathrm{t}}\mathrm{dt}\:=\mathrm{I}−\mathrm{J} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\mathrm{dt}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \mathrm{t}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\left[\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}^{\mathrm{2}} \mathrm{t}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}×\frac{\mathrm{2lnt}}{\mathrm{t}}\:\mathrm{dt} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\left\{\:\left[\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{lnt}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\:\mathrm{dt}\right\} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\left\{−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\right\}\:=\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\mathrm{I}\:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} }\:=\mathrm{2}\xi\left(\mathrm{3}\right) \\ $$$$\mathrm{J}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\mathrm{dt}\:?\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{J}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \mathrm{t}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{n}} \mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:\:\mathrm{but}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{ln}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\left[\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}^{\mathrm{2}} \mathrm{t}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}×\frac{\mathrm{2lnt}}{\mathrm{t}}\:\mathrm{dt}\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\:−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{t}^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\left\{\:\left[\frac{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{t}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{t}^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)}\left\{\frac{−\mathrm{ln2}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\right\} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\:+\frac{\mathrm{2ln2}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{2}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} \mathrm{2}^{\mathrm{n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\mathrm{J}\:=\mathrm{ln}^{\mathrm{2}} \mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{n}+\mathrm{1}} }+\mathrm{2ln2}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{2}^{\mathrm{n}+\mathrm{1}} }−\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} \mathrm{2}^{\mathrm{n}+\mathrm{1}} } \\ $$$$=\mathrm{ln}^{\mathrm{2}} \mathrm{2}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}\:\mathrm{2}^{\mathrm{n}} }\:+\mathrm{2ln}\left(\mathrm{2}\right)\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \:\mathrm{2}^{\mathrm{n}} }\:−\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} \mathrm{2}^{\mathrm{n}} } \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{those}\:\mathrm{series}\:…\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by mnjuly1970 last updated on 30/Aug/20
$${thank}\:{you}\:{so}\:{much}\:{sir}… \\ $$
Commented by mathmax by abdo last updated on 30/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
