Question Number 111429 by mnjuly1970 last updated on 03/Sep/20
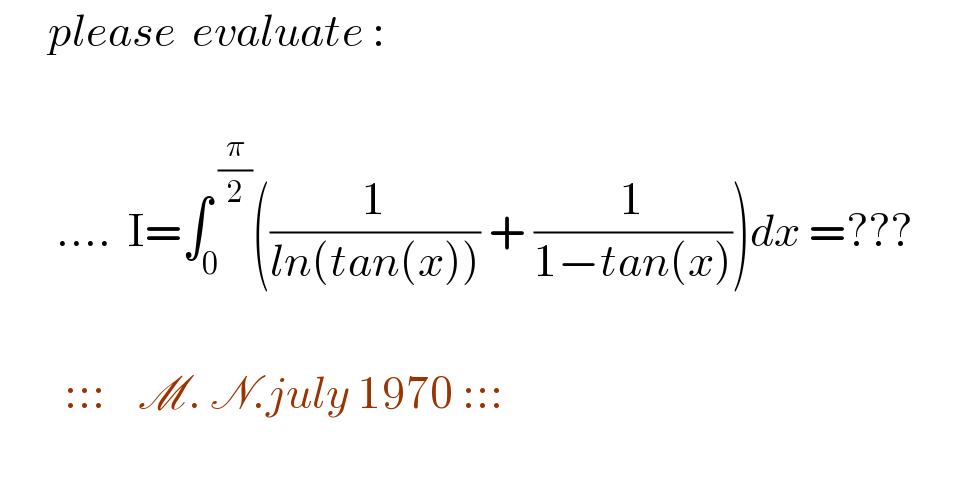
$$\:\:\:\:\:\:{please}\:\:{evaluate}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:….\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{{ln}\left({tan}\left({x}\right)\right)}\:+\:\frac{\mathrm{1}}{\mathrm{1}−{tan}\left({x}\right)}\right){dx}\:=??? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\::::\:\:\:\:\mathscr{M}.\:\mathscr{N}.{july}\:\mathrm{1970}\:::: \\ $$$$\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 03/Sep/20

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{log}\left({sinx}\right)−{log}\left({cosx}\right)}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}−{tanx}}{dx} \\ $$$$={I}_{{a}} +{I}_{{b}} =−\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{log}\left({sinx}\right)−{log}\left({cosx}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{log}\left({cosx}\right)−{log}\left({sinx}\right)}={I}_{{a}} \\ $$$$\mathrm{2}{I}_{{a}} =\mathrm{0}\Rightarrow{I}_{{a}} =\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sinx}}{{cosx}−{sinx}}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{sinx}−{cosx}}={I}_{{a}} \\ $$$$\mathrm{2}{I}_{{a}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}−{sinx}}{{sinx}−{cosx}} \\ $$$${I}_{{a}} =−\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20
![solution: Ω=∫_0 ^( (π/2)) [(1/(log(tan(x))))+(1/(1−tan(x)))]dx =^(∫_a ^b f(x)dx=∫_(a ) ^( b) f(a+b−x)dx) ∫_0 ^( (π/2)) [(1/(−log(tan(x))))+((tan(x)+1−1)/(tan(x)−1))]dx =−Ω+(π/2)⇒Ω=(1/4) π .... ✓✓](https://www.tinkutara.com/question/Q111472.png)
$${solution}: \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left[\frac{\mathrm{1}}{{log}\left({tan}\left({x}\right)\right)}+\frac{\mathrm{1}}{\mathrm{1}−{tan}\left({x}\right)}\right]{dx} \\ $$$$\overset{\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}\:} ^{\:{b}} {f}\left({a}+{b}−{x}\right){dx}} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left[\frac{\mathrm{1}}{−{log}\left({tan}\left({x}\right)\right)}+\frac{{tan}\left({x}\right)+\mathrm{1}−\mathrm{1}}{{tan}\left({x}\right)−\mathrm{1}}\right]{dx} \\ $$$$=−\Omega+\frac{\pi}{\mathrm{2}}\Rightarrow\Omega=\frac{\mathrm{1}}{\mathrm{4}}\:\pi\:….\:\checkmark\checkmark \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20

$$\checkmark{correct}. \\ $$
Commented by Dwaipayan Shikari last updated on 03/Sep/20

$${Answer}\:{is}\:\frac{\pi}{\mathrm{4}} \\ $$
Commented by mathdave last updated on 03/Sep/20
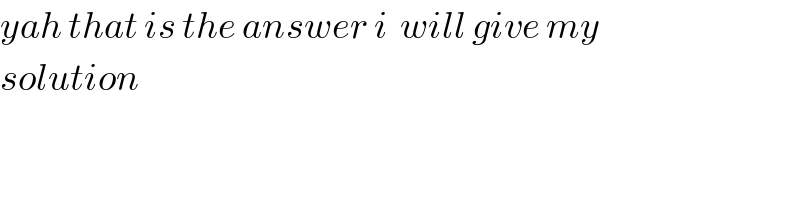
$${yah}\:{that}\:{is}\:{the}\:{answer}\:{i}\:\:{will}\:{give}\:{my} \\ $$$${solution}\: \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20
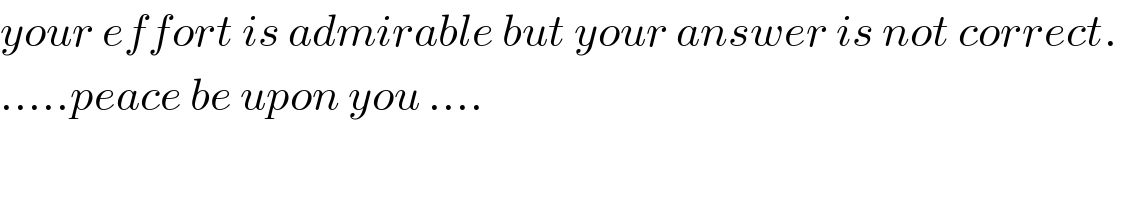
$${your}\:{effort}\:{is}\:{admirable}\:{but}\:{your}\:{answer}\:{is}\:{not}\:{correct}.\: \\ $$$$…..{peace}\:{be}\:{upon}\:{you}\:…. \\ $$$$\: \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20
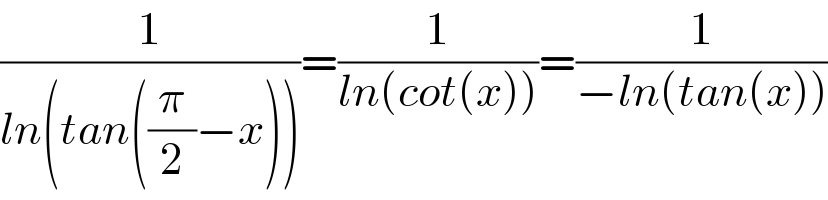
$$\frac{\mathrm{1}}{{ln}\left({tan}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)}=\frac{\mathrm{1}}{{ln}\left({cot}\left({x}\right)\right)}=\frac{\mathrm{1}}{−{ln}\left({tan}\left({x}\right)\right)} \\ $$
Commented by mathdave last updated on 03/Sep/20
$${yah}\:{u}\:{are}\:{very}\:{right} \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20

$${thak}\:{you}. \\ $$
