Question Number 121649 by mnjuly1970 last updated on 10/Nov/20
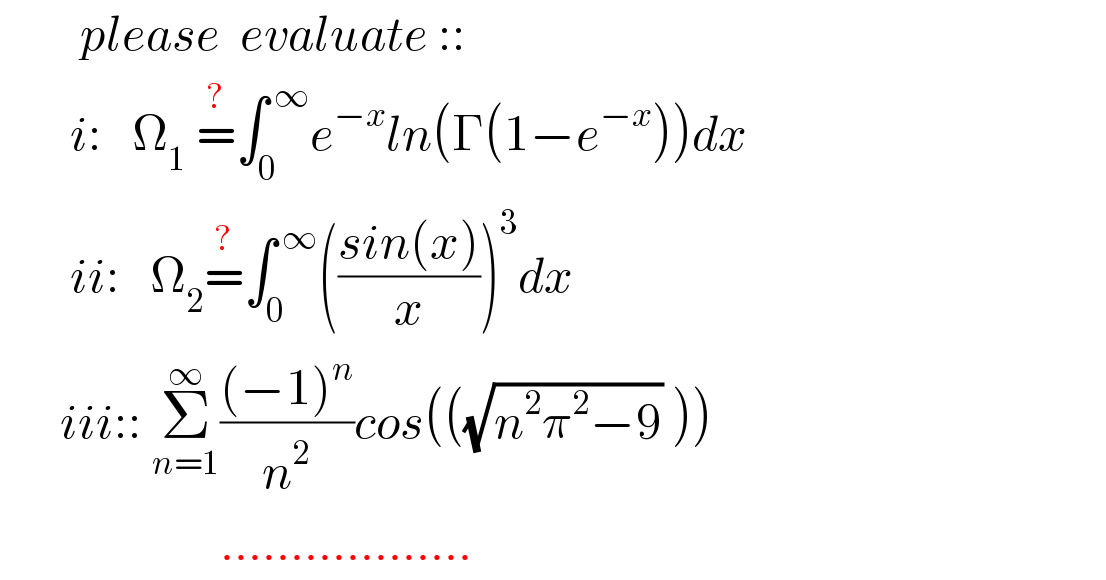
$$\:\:\:\:\:\:\:\:{please}\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:{i}:\:\:\:\Omega_{\mathrm{1}} \:\overset{?} {=}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}} {ln}\left(\Gamma\left(\mathrm{1}−{e}^{−{x}} \right)\right){dx} \\ $$$$\:\:\:\:\:\:\:{ii}:\:\:\:\Omega_{\mathrm{2}} \overset{?} {=}\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{sin}\left({x}\right)}{{x}}\right)^{\mathrm{3}} {dx} \\ $$$$\:\:\:\:\:\:{iii}::\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }{cos}\left(\left(\sqrt{{n}^{\mathrm{2}} \pi^{\mathrm{2}} −\mathrm{9}}\:\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……………… \\ $$
Commented by Dwaipayan Shikari last updated on 10/Nov/20
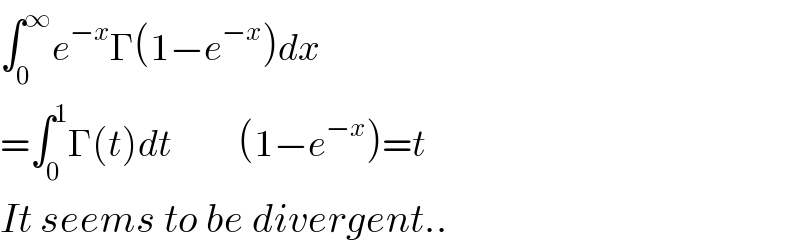
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} \Gamma\left(\mathrm{1}−{e}^{−{x}} \right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \Gamma\left({t}\right){dt}\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}−{e}^{−{x}} \right)={t} \\ $$$${It}\:{seems}\:{to}\:{be}\:{divergent}.. \\ $$
Commented by mnjuly1970 last updated on 10/Nov/20
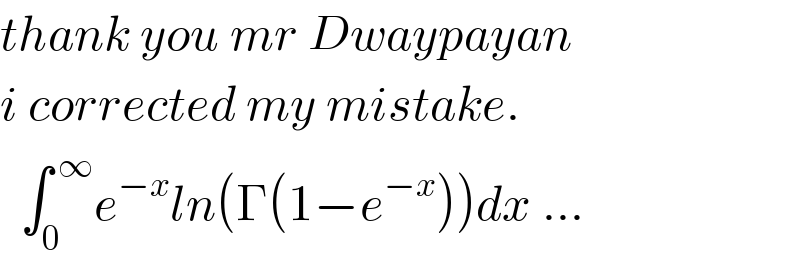
$${thank}\:{you}\:{mr}\:{Dwaypayan} \\ $$$${i}\:{corrected}\:{my}\:{mistake}. \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}} {ln}\left(\Gamma\left(\mathrm{1}−{e}^{−{x}} \right)\right){dx}\:… \\ $$
Answered by mnjuly1970 last updated on 11/Nov/20

