Menu Close

please-evaluate-x-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 121680 by aristarque last updated on 10/Nov/20
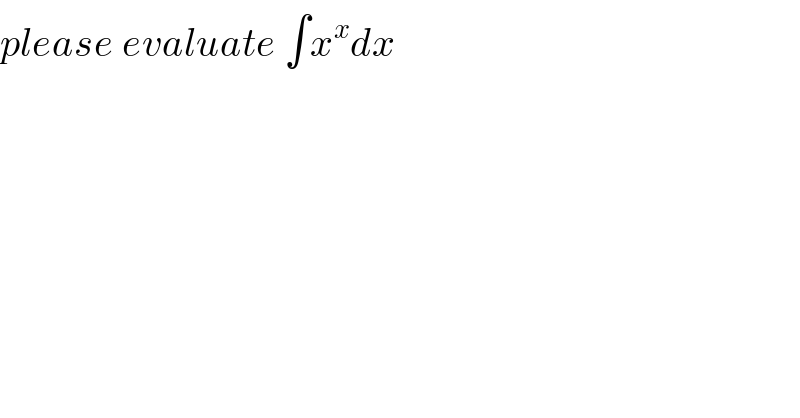
please evaluate ∫x^x dx
$${please}\:{evaluate}\:\int{x}^{{x}} {dx} \\ $$
Answered by Dwaipayan Shikari last updated on 11/Nov/20
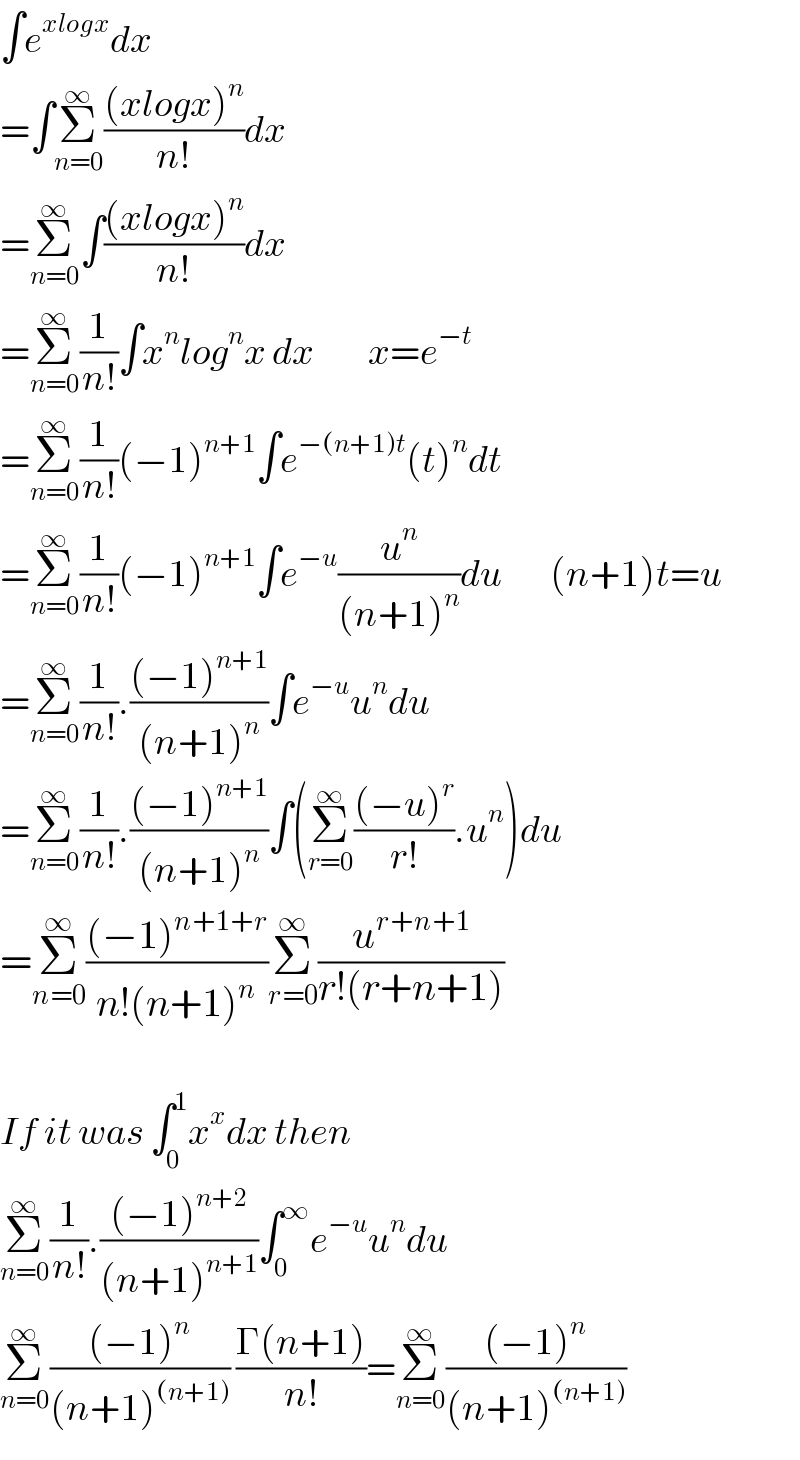
∫e^(xlogx) dx =∫Σ_(n=0) ^∞ (((xlogx)^n )/(n!))dx =Σ_(n=0) ^∞ ∫(((xlogx)^n )/(n!))dx =Σ_(n=0) ^∞ (1/(n!))∫x^n log^n x dx x=e^(−t) =Σ_(n=0) ^∞ (1/(n!))(−1)^(n+1) ∫e^(−(n+1)t) (t)^n dt =Σ_(n=0) ^∞ (1/(n!))(−1)^(n+1) ∫e^(−u) (u^n /((n+1)^n ))du (n+1)t=u =Σ_(n=0) ^∞ (1/(n!)).(((−1)^(n+1) )/((n+1)^n ))∫e^(−u) u^n du =Σ_(n=0) ^∞ (1/(n!)).(((−1)^(n+1) )/((n+1)^n ))∫(Σ_(r=0) ^∞ (((−u)^r )/(r!)).u^n )du =Σ_(n=0) ^∞ (((−1)^(n+1+r) )/(n!(n+1)^n ))Σ_(r=0) ^∞ (u^(r+n+1) /(r!(r+n+1))) If it was ∫_0 ^1 x^x dx then Σ_(n=0) ^∞ (1/(n!)).(((−1)^(n+2) )/((n+1)^(n+1) ))∫_0 ^∞ e^(−u) u^n du Σ_(n=0) ^∞ (((−1)^n )/((n+1)^((n+1)) )) ((Γ(n+1))/(n!))=Σ_(n=0) ^∞ (((−1)^n )/((n+1)^((n+1)) ))
$$\int{e}^{{xlogx}} {dx} \\ $$$$=\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({xlogx}\right)^{{n}} }{{n}!}{dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int\frac{\left({xlogx}\right)^{{n}} }{{n}!}{dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int{x}^{{n}} {log}^{{n}} {x}\:{dx}\:\:\:\:\:\:\:\:\:{x}={e}^{−{t}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int{e}^{−\left({n}+\mathrm{1}\right){t}} \left({t}\right)^{{n}} {dt} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int{e}^{−{u}} \frac{{u}^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}} }{du}\:\:\:\:\:\:\:\:\left({n}+\mathrm{1}\right){t}={u} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}.\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{{n}} }\int{e}^{−{u}} {u}^{{n}} {du} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}.\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{{n}} }\int\left(\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{u}\right)^{{r}} }{{r}!}.{u}^{{n}} \right){du}\: \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}+{r}} }{{n}!\left({n}+\mathrm{1}\right)^{{n}} }\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{r}+{n}+\mathrm{1}} }{{r}!\left({r}+{n}+\mathrm{1}\right)} \\ $$$$ \\ $$$${If}\:{it}\:{was}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{x}} {dx}\:{then} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}.\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{2}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {u}^{{n}} {du} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{\left({n}+\mathrm{1}\right)} }\:\frac{\Gamma\left({n}+\mathrm{1}\right)}{{n}!}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{\left({n}+\mathrm{1}\right)} } \\ $$
Commented by aristarque last updated on 11/Nov/20
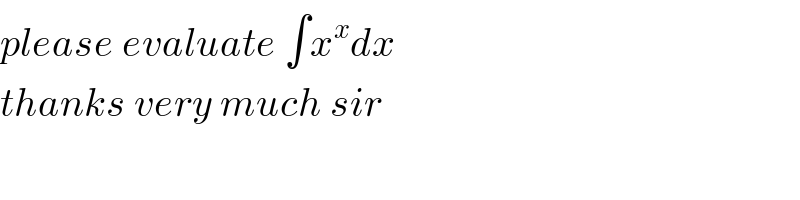
please evaluate ∫x^x dx thanks very much sir
$${please}\:{evaluate}\:\int{x}^{{x}} {dx} \\ $$$${thanks}\:{very}\:{much}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Nov/20
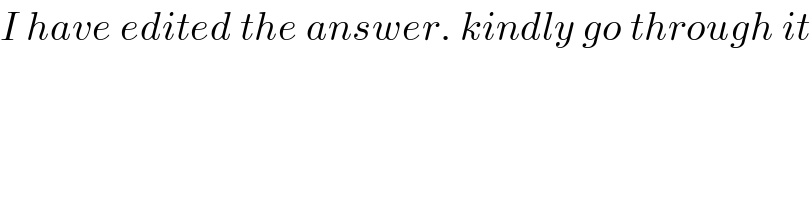
I have edited the answer. kindly go through it
$${I}\:{have}\:{edited}\:{the}\:{answer}.\:{kindly}\:{go}\:{through}\:{it} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *