Menu Close

Please-explain-1-i-lt-j-n-ij-j-2-n-j-j-1-j-2-I-want-to-know-how-L-H-S-R-H-S-

Tinku Tara 0 Comments
Pin




Question Number 98844 by I want to learn more last updated on 16/Jun/20
Please explain: Σ_(1 ≤ i < j ≤ n) ij = Σ_(j = 2) ^n ((j(j − 1)j)/2) I want to know how L.H.S = R.H.S
$$\mathrm{Please}\:\mathrm{explain}:\:\:\:\:\:\:\underset{\mathrm{1}\:\leqslant\:\boldsymbol{\mathrm{i}}\:<\:\boldsymbol{\mathrm{j}}\:\leqslant\:\boldsymbol{\mathrm{n}}} {\sum}\boldsymbol{\mathrm{ij}}\:\:\:\:=\:\:\:\underset{\boldsymbol{\mathrm{j}}\:\:=\:\:\mathrm{2}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\frac{\boldsymbol{\mathrm{j}}\left(\boldsymbol{\mathrm{j}}\:−\:\mathrm{1}\right)\boldsymbol{\mathrm{j}}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{I}}\:\mathrm{want}\:\mathrm{to}\:\mathrm{know}\:\mathrm{how}\:\mathrm{L}.\mathrm{H}.\mathrm{S}\:\:=\:\:\mathrm{R}.\mathrm{H}.\mathrm{S} \\ $$
Answered by mr W last updated on 16/Jun/20
Σ_(1≤i<j≤n) ij =Σ_(i=1) ^(n−1) (iΣ_(j=i+1) ^n j) =Σ_(i=1) ^(n−1) [i×(((n+i+1)(n−i))/2)] or =Σ_(i=2) ^n (jΣ_(i=1) ^(j−1) i) =Σ_(i=2) ^n (j×((j×(j−1))/2)) =Σ_(j=2) ^n ((j^2 (j−1))/2)
$$\underset{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} {\sum}{ij} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left({i}\underset{{j}={i}+\mathrm{1}} {\overset{{n}} {\sum}}{j}\right) \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[{i}×\frac{\left({n}+{i}+\mathrm{1}\right)\left({n}−{i}\right)}{\mathrm{2}}\right] \\ $$$${or} \\ $$$$=\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}\left({j}\underset{{i}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}{i}\right) \\ $$$$=\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}\left({j}×\frac{{j}×\left({j}−\mathrm{1}\right)}{\mathrm{2}}\right) \\ $$$$=\underset{{j}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{{j}^{\mathrm{2}} \left({j}−\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by I want to learn more last updated on 16/Jun/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by I want to learn more last updated on 16/Jun/20
Commented by I want to learn more last updated on 16/Jun/20
Sir my problems the red ink. How can we know it. why we have: Σ j Σ_(i = 1) ^(j − 1) i = Σ_(j = 2) ^n ... = Σ_(j = 1) ^n ?????? And what is the difference in 1 ≤ i < j ≤ n and 1 ≤ i ≤ j ≤ n
$$\mathrm{Sir}\:\mathrm{my}\:\mathrm{problems}\:\mathrm{the}\:\mathrm{red}\:\mathrm{ink}.\:\mathrm{How}\:\mathrm{can}\:\mathrm{we}\:\mathrm{know}\:\mathrm{it}. \\ $$$$\mathrm{why}\:\mathrm{we}\:\mathrm{have}:\:\:\:\:\Sigma\:\mathrm{j}\:\underset{\mathrm{i}\:=\:\mathrm{1}} {\overset{\mathrm{j}\:−\:\mathrm{1}} {\sum}}\mathrm{i}\:\:\:\:=\:\:\:\underset{\mathrm{j}\:=\:\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\:…\:\:\:\:=\:\:\:\underset{\mathrm{j}\:\:=\:\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\:\:\:\:\:\:\:?????? \\ $$$$ \\ $$$$\mathrm{And}\:\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{difference}\:\mathrm{in} \\ $$$$\:\:\:\:\mathrm{1}\:\leqslant\:\mathrm{i}\:<\:\mathrm{j}\:\leqslant\:\mathrm{n}\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\:\mathrm{1}\:\leqslant\:\mathrm{i}\:\leqslant\:\mathrm{j}\:\leqslant\:\mathrm{n} \\ $$
Commented by mr W last updated on 16/Jun/20
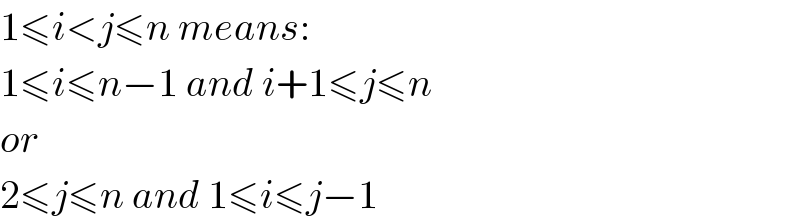
1≤i<j≤n means: 1≤i≤n−1 and i+1≤j≤n or 2≤j≤n and 1≤i≤j−1
$$\mathrm{1}\leqslant{i}<{j}\leqslant{n}\:{means}: \\ $$$$\mathrm{1}\leqslant{i}\leqslant{n}−\mathrm{1}\:{and}\:{i}+\mathrm{1}\leqslant{j}\leqslant{n} \\ $$$${or} \\ $$$$\mathrm{2}\leqslant{j}\leqslant{n}\:{and}\:\mathrm{1}\leqslant{i}\leqslant{j}−\mathrm{1} \\ $$
Commented by I want to learn more last updated on 16/Jun/20
Ohh. Thanks sir. I really appreciate
$$\mathrm{Ohh}.\:\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate} \\ $$
Commented by mr W last updated on 16/Jun/20
Commented by mr W last updated on 16/Jun/20
red marked combinations are 1≤i<j≤n they can be described as 1≤i≤n−1 and i+1≤j≤n or as 2≤j≤n and 1≤i≤j−1
$${red}\:{marked}\:{combinations}\:{are} \\ $$$$\mathrm{1}\leqslant{i}<{j}\leqslant{n} \\ $$$$ \\ $$$${they}\:{can}\:{be}\:{described}\:{as} \\ $$$$\mathrm{1}\leqslant{i}\leqslant{n}−\mathrm{1}\:{and}\:{i}+\mathrm{1}\leqslant{j}\leqslant{n} \\ $$$${or}\:{as} \\ $$$$\mathrm{2}\leqslant{j}\leqslant{n}\:{and}\:\mathrm{1}\leqslant{i}\leqslant{j}−\mathrm{1} \\ $$
Commented by I want to learn more last updated on 16/Jun/20
wow, thanks sir for more details.
$$\mathrm{wow},\:\mathrm{thanks}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{more}\:\mathrm{details}. \\ $$
Answered by mathmax by abdo last updated on 16/Jun/20
Σ_(1≤i<j≤n) ij = Σ_(j=1) ^n (Σ_(i=1) ^(j−1) ij) =Σ_(j=1) ^n j((((j−1)j)/2)) =Σ_(j=1) ^n ((j^2 (j−1))/2) =(1/2)(Σ_(j=1) ^n j^3 −Σ_(j=1) ^n j^2 ) =(1/2){ ((n^2 (n+1)^2 )/4)−((n(n+1)(2n+1))/6)} =((n(n+1))/2){ ((n(n+1))/4)−((2n+1)/6)} =((n(n+1))/2){((3n(n+1)−2(2n+1))/(12))} =((n(n+1)(3n^2 −n−2))/(24))
$$\sum_{\mathrm{1}\leqslant\mathrm{i}<\mathrm{j}\leqslant\mathrm{n}} \mathrm{ij}\:=\:\sum_{\mathrm{j}=\mathrm{1}} ^{\mathrm{n}} \left(\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{j}−\mathrm{1}} \:\mathrm{ij}\right)\:=\sum_{\mathrm{j}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{j}\left(\frac{\left(\mathrm{j}−\mathrm{1}\right)\mathrm{j}}{\mathrm{2}}\right)\:=\sum_{\mathrm{j}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{j}^{\mathrm{2}} \left(\mathrm{j}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\sum_{\mathrm{j}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{j}^{\mathrm{3}} −\sum_{\mathrm{j}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{j}^{\mathrm{2}} \right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\right\} \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\left\{\:\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{4}}−\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{6}}\right\}\:=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\left\{\frac{\mathrm{3n}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{2}\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{12}}\right\} \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{3n}^{\mathrm{2}} −\mathrm{n}−\mathrm{2}\right)}{\mathrm{24}} \\ $$
Commented by I want to learn more last updated on 17/Jun/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 17/Jun/20
you are welcome
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mathmax by abdo last updated on 16/Jun/20
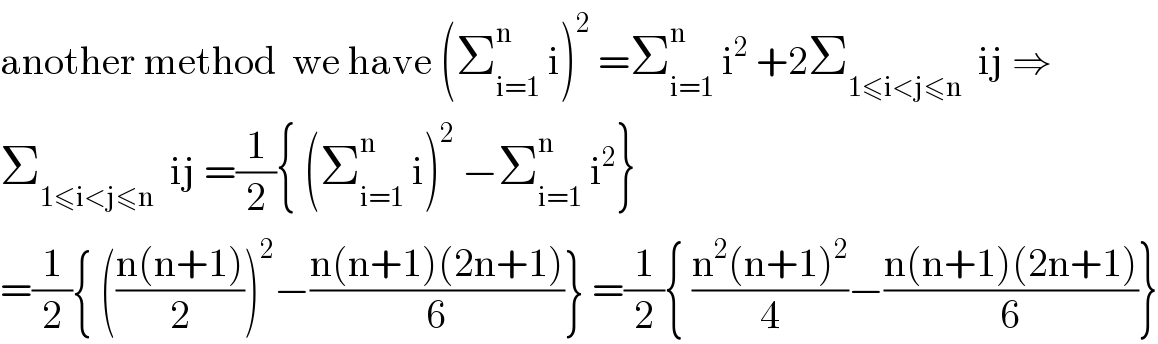
another method we have (Σ_(i=1) ^n i)^2 =Σ_(i=1) ^n i^2 +2Σ_(1≤i<j≤n) ij ⇒ Σ_(1≤i<j≤n) ij =(1/2){ (Σ_(i=1) ^n i)^2 −Σ_(i=1) ^n i^2 } =(1/2){ (((n(n+1))/2))^2 −((n(n+1)(2n+1))/6)} =(1/2){ ((n^2 (n+1)^2 )/4)−((n(n+1)(2n+1))/6)}
$$\mathrm{another}\:\mathrm{method}\:\:\mathrm{we}\:\mathrm{have}\:\left(\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{i}\right)^{\mathrm{2}} \:=\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{i}^{\mathrm{2}} \:+\mathrm{2}\sum_{\mathrm{1}\leqslant\mathrm{i}<\mathrm{j}\leqslant\mathrm{n}} \:\:\mathrm{ij}\:\Rightarrow \\ $$$$\sum_{\mathrm{1}\leqslant\mathrm{i}<\mathrm{j}\leqslant\mathrm{n}} \:\:\mathrm{ij}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left(\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{i}\right)^{\mathrm{2}} \:−\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{i}^{\mathrm{2}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left(\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\right\} \\ $$
Commented by I want to learn more last updated on 17/Jun/20
Thanks sir
$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *