Menu Close

please-find-the-value-of-sin-2-7-sin-4-7-sin-8-7-

Tinku Tara 0 Comments
Pin




Question Number 144169 by gsk2684 last updated on 22/Jun/21
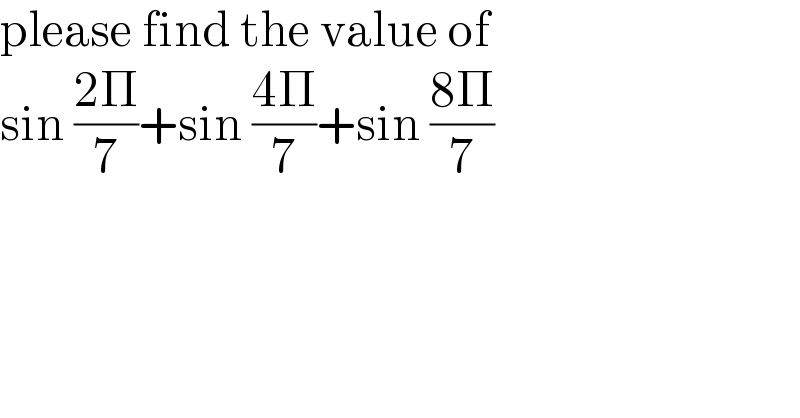
please find the value of sin ((2Π)/7)+sin ((4Π)/7)+sin ((8Π)/7)
$$\mathrm{please}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\mathrm{sin}\:\frac{\mathrm{2}\Pi}{\mathrm{7}}+\mathrm{sin}\:\frac{\mathrm{4}\Pi}{\mathrm{7}}+\mathrm{sin}\:\frac{\mathrm{8}\Pi}{\mathrm{7}} \\ $$
Commented by justtry last updated on 23/Jun/21
Answered by mindispower last updated on 23/Jun/21
sin(a)+sin(b)=2cos(((a−b)/2))sin(((a+b)/2)) =sin(((2π)/7))+2cos(((2π)/7))sin(((6π)/7)) =2sin((π/7))(cos((π/7))+cos(((2π)/7))) 4sin((π/7))cos((π/(14)))cos(((3π)/(14))) =4cos(((5π)/(14)))cos((π/(14)))cos(((3π)/(14)))=S S^2 =−16cos((π/(14)))cos(((13π)/(14)))cos(((3π)/(14)))cos(((11π)/(14)))cos(((5π)/(14)))cos(((9π)/(14))) just using cos(π−x)=−cos(x) z^7 +1=0⇒z=e^(i(((π+2kπ)/7))) ,k∈{0,6} z^7 +1=Π_(k=0) ^6 (z−e^((i(1+2k)π)/7) ) (z+1)(z^6 −z^5 +z^4 −z^3 +z^2 −z+1)=(z+1)Π_(k=0,k≠3) ^6 (z−e^(i(((1+2k)π)/7)) ) ⇒Σ_(k=0) ^6 (−z)^k =Π_(k=0,k≠3) ^6 (z−e^(((1+2k)iπ)/7) ) z=−1 ⇒7=Π(1+e^((i(1+2k)π)/7) )=Π_(k=0,k≠3) ^6 .e^(i(1+2k)(π/(14))) (e^((i(1+2k)π)/(14)) +e^((−i(1+2k)π)/(14)) ) ⇒7=2^6 .e^((i(1+3+5+9+11+13)π)/(14)) .Π_(k=,k≠3) ^6 cos(((1+2k)/(14))π)_(=S′) 7=2^6 .e^(i(3π)) .S S′=−(7/(64)) S′=−(S^2 /(16)) ⇒−(S^2 /(16))=−(7/(64))⇒S^2 =(7/4),S∈{((√7)/2),−((√7)/2) (π/(14)),((3π)/(14)),((5π)/(14))∈[0,(π/2)[⇒S>0 S=sin(((2π)/7))+sin(((4π)/7))+sin(((8π)/7))=((√7)/2)
$${sin}\left({a}\right)+{sin}\left({b}\right)=\mathrm{2}{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right){sin}\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$$$={sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+\mathrm{2}{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right){sin}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right) \\ $$$$=\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{7}}\right)\left({cos}\left(\frac{\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\right) \\ $$$$\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{7}}\right){cos}\left(\frac{\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{3}\pi}{\mathrm{14}}\right) \\ $$$$=\mathrm{4}{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{14}}\right){cos}\left(\frac{\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{3}\pi}{\mathrm{14}}\right)={S} \\ $$$${S}^{\mathrm{2}} =−\mathrm{16}{cos}\left(\frac{\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{13}\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{3}\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{11}\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{5}\pi}{\mathrm{14}}\right){cos}\left(\frac{\mathrm{9}\pi}{\mathrm{14}}\right) \\ $$$${just}\:{using}\:{cos}\left(\pi−{x}\right)=−{cos}\left({x}\right) \\ $$$$ \\ $$$$ \\ $$$${z}^{\mathrm{7}} +\mathrm{1}=\mathrm{0}\Rightarrow{z}={e}^{{i}\left(\frac{\pi+\mathrm{2}{k}\pi}{\mathrm{7}}\right)} ,{k}\in\left\{\mathrm{0},\mathrm{6}\right\} \\ $$$${z}^{\mathrm{7}} +\mathrm{1}=\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\prod}}\left({z}−{e}^{\frac{{i}\left(\mathrm{1}+\mathrm{2}{k}\right)\pi}{\mathrm{7}}} \right) \\ $$$$\left({z}+\mathrm{1}\right)\left({z}^{\mathrm{6}} −{z}^{\mathrm{5}} +{z}^{\mathrm{4}} −{z}^{\mathrm{3}} +{z}^{\mathrm{2}} −{z}+\mathrm{1}\right)=\left({z}+\mathrm{1}\right)\underset{{k}=\mathrm{0},{k}\neq\mathrm{3}} {\overset{\mathrm{6}} {\prod}}\left({z}−{e}^{{i}\frac{\left(\mathrm{1}+\mathrm{2}{k}\right)\pi}{\mathrm{7}}} \right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\left(−{z}\right)^{{k}} =\underset{{k}=\mathrm{0},{k}\neq\mathrm{3}} {\overset{\mathrm{6}} {\prod}}\left({z}−{e}^{\frac{\left(\mathrm{1}+\mathrm{2}{k}\right){i}\pi}{\mathrm{7}}} \right) \\ $$$${z}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{7}=\Pi\left(\mathrm{1}+{e}^{\frac{{i}\left(\mathrm{1}+\mathrm{2}{k}\right)\pi}{\mathrm{7}}} \right)=\underset{{k}=\mathrm{0},{k}\neq\mathrm{3}} {\overset{\mathrm{6}} {\prod}}.{e}^{{i}\left(\mathrm{1}+\mathrm{2}{k}\right)\frac{\pi}{\mathrm{14}}} \left({e}^{\frac{{i}\left(\mathrm{1}+\mathrm{2}{k}\right)\pi}{\mathrm{14}}} +{e}^{\frac{−{i}\left(\mathrm{1}+\mathrm{2}{k}\right)\pi}{\mathrm{14}}} \right) \\ $$$$\Rightarrow\mathrm{7}=\mathrm{2}^{\mathrm{6}} .{e}^{\frac{{i}\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+\mathrm{9}+\mathrm{11}+\mathrm{13}\right)\pi}{\mathrm{14}}} .\underset{{k}=,{k}\neq\mathrm{3}} {\overset{\mathrm{6}} {\prod}}{cos}\left(\frac{\mathrm{1}+\mathrm{2}{k}}{\mathrm{14}}\pi\underset{={S}'} {\right)} \\ $$$$\mathrm{7}=\mathrm{2}^{\mathrm{6}} .{e}^{{i}\left(\mathrm{3}\pi\right)} .{S} \\ $$$${S}'=−\frac{\mathrm{7}}{\mathrm{64}} \\ $$$${S}'=−\frac{{S}^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\Rightarrow−\frac{{S}^{\mathrm{2}} }{\mathrm{16}}=−\frac{\mathrm{7}}{\mathrm{64}}\Rightarrow{S}^{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{4}},{S}\in\left\{\frac{\sqrt{\mathrm{7}}}{\mathrm{2}},−\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right. \\ $$$$\frac{\pi}{\mathrm{14}},\frac{\mathrm{3}\pi}{\mathrm{14}},\frac{\mathrm{5}\pi}{\mathrm{14}}\in\left[\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\Rightarrow{S}>\mathrm{0}\right.\right. \\ $$$${S}={sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+{sin}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+{sin}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *