Question Number 49857 by afachri last updated on 11/Dec/18

Commented by maxmathsup by imad last updated on 11/Dec/18
![the best way is this let A(x)=∣x−2∣−3∣x+7∣ (e) ⇔ A(x)<0 we eradicate the abslutevalue x −∞ −7 2 +∞ ∣x−2∣ −x+2 −x+2 0 x−2 ∣x+7∣ −x−7 0 x+7 x+7 A(x) 2x+23 −4x−19 −2x−23 case 1 x≤−7 (e) ⇔ 2x+23 <0 ⇔ x<−((23)/2) ⇒ S_1 =]−∞ ,−((23)/2)[ case 2 −7≤x≤2 (e) ⇔ −4x −19 <0 ⇔ −4x<19 ⇔4x >−19 ⇔x>−((19)/4) ⇒ S_2 =]−((19)/4) ,2] case 3 x≥2 ⇒ (e)⇔−2x −23 <0 ⇔ −2x<23 ⇔ 2x>−23 ⇔x>−((23)/2) ⇒S_3 =[2,+∞[ and we take ∪S_i S=S_1 ∪S_2 ∪ S_3 =]−∞,−((23)/2)[∪]−((19)/4),+∞[ .](https://www.tinkutara.com/question/Q49880.png)
Commented by afachri last updated on 11/Dec/18

Commented by afachri last updated on 11/Dec/18
Commented by Abdo msup. last updated on 12/Dec/18

Answered by hassentimol last updated on 11/Dec/18
![Well... We write it as : ∣x−2∣ − 3∣x+7∣ < 0 We have : { ((x−2 > 0 ⇔ x > 2)),((x+7 > 0 ⇔ x > −7)) :} Therefore we define I_1 , I_2 and I_3 such as : I_1 = ]−∞,−7] : −x+2+3x+21 = 2x+23 I_2 =[−7,2] : −x+2−3x−21 = −4x−19 I_3 =[2,+∞[ : x−2−3x−21 = −2x−23 We have : Let S_n be the set of solutions for the I_n interval. For I_1 : 2x+23<0 ⇔ x<((−23)/2) : S_1 =]−∞,((−23)/2)[ For I_2 : −4x−19<0 ⇔ x>((−19)/4) : S_2 =[((−19)/4),2[ For I_3 : −2x−23<0 ⇔ x>((−23)/2) : S_3 =[2,+∞[ Finally : We can consider S the set of solutions : S = { x ∣ x∈]−∞, ((−19)/4)[ ∪ ]2_ ^ , +∞[ } In other terms : Either x<((−19)/4) , either x>2. Thanks T.H.](https://www.tinkutara.com/question/Q49858.png)
Commented by afachri last updated on 11/Dec/18
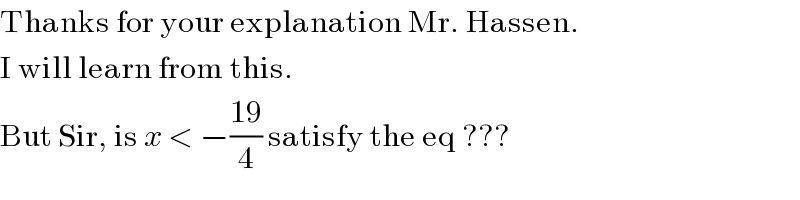
Commented by hassentimol last updated on 11/Dec/18
Commented by hassentimol last updated on 11/Dec/18
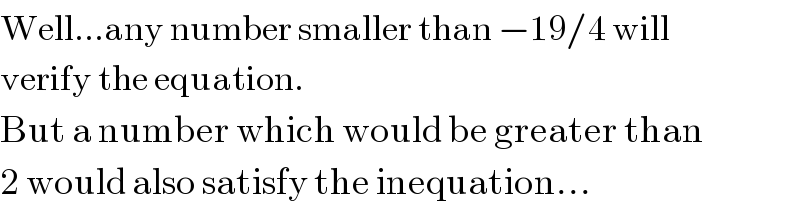
Commented by hassentimol last updated on 11/Dec/18

Commented by hassentimol last updated on 11/Dec/18

Commented by afachri last updated on 11/Dec/18
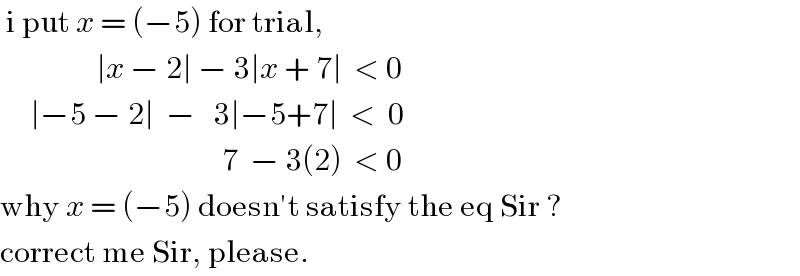
Commented by afachri last updated on 11/Dec/18

Commented by afachri last updated on 11/Dec/18

