Question Number 117552 by sandy_delta last updated on 12/Oct/20
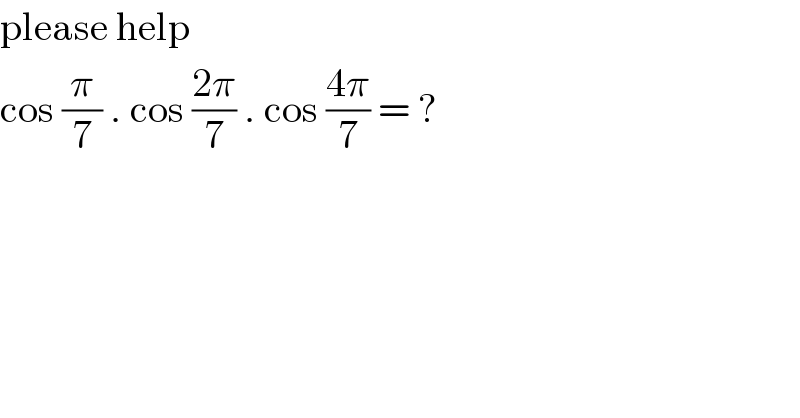
$$\mathrm{please}\:\mathrm{help} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{7}}\:.\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\:.\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{7}}\:=\:? \\ $$
Commented by TANMAY PANACEA last updated on 12/Oct/20
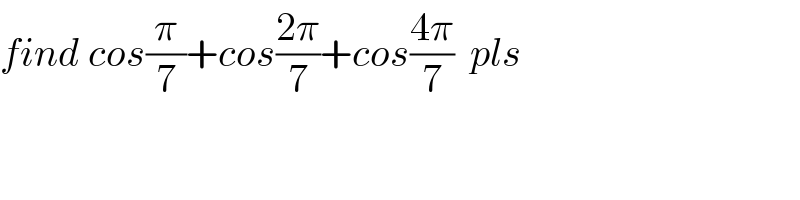
$${find}\:{cos}\frac{\pi}{\mathrm{7}}+{cos}\frac{\mathrm{2}\pi}{\mathrm{7}}+{cos}\frac{\mathrm{4}\pi}{\mathrm{7}}\:\:{pls} \\ $$
Answered by AbduraufKodiriy last updated on 12/Oct/20
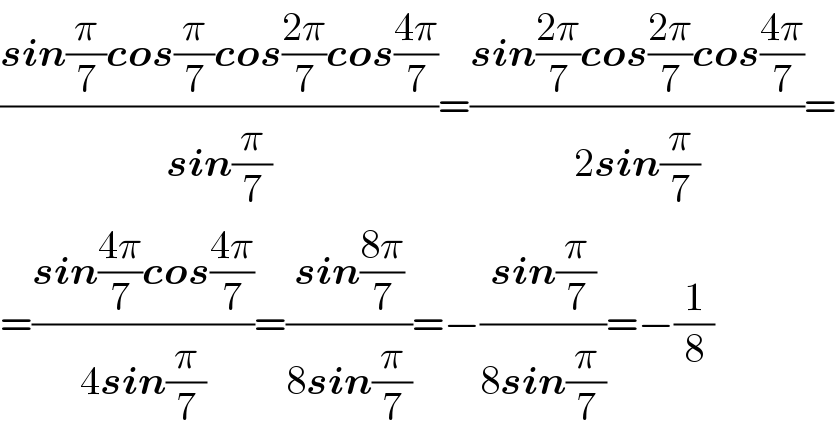
$$\frac{\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}\boldsymbol{{cos}}\frac{\pi}{\mathrm{7}}\boldsymbol{{cos}}\frac{\mathrm{2}\pi}{\mathrm{7}}\boldsymbol{{cos}}\frac{\mathrm{4}\pi}{\mathrm{7}}}{\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}}=\frac{\boldsymbol{{sin}}\frac{\mathrm{2}\pi}{\mathrm{7}}\boldsymbol{{cos}}\frac{\mathrm{2}\pi}{\mathrm{7}}\boldsymbol{{cos}}\frac{\mathrm{4}\pi}{\mathrm{7}}}{\mathrm{2}\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}}= \\ $$$$=\frac{\boldsymbol{{sin}}\frac{\mathrm{4}\pi}{\mathrm{7}}\boldsymbol{{cos}}\frac{\mathrm{4}\pi}{\mathrm{7}}}{\mathrm{4}\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}}=\frac{\boldsymbol{{sin}}\frac{\mathrm{8}\pi}{\mathrm{7}}}{\mathrm{8}\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}}=−\frac{\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}}{\mathrm{8}\boldsymbol{{sin}}\frac{\pi}{\mathrm{7}}}=−\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by sandy_delta last updated on 12/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Oct/20
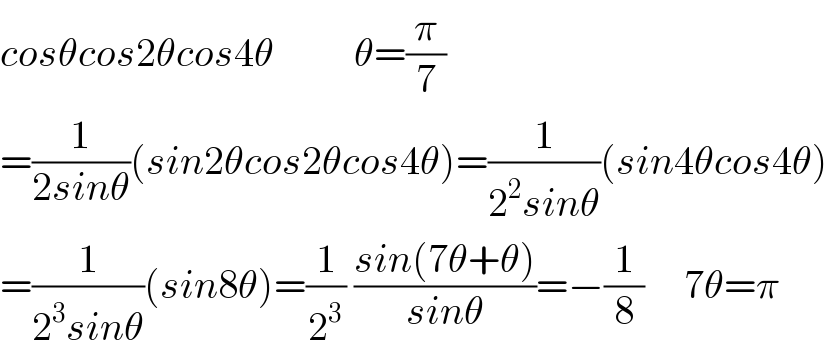
$${cos}\theta{cos}\mathrm{2}\theta{cos}\mathrm{4}\theta\:\:\:\:\:\:\:\:\:\:\theta=\frac{\pi}{\mathrm{7}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{sin}\theta}\left({sin}\mathrm{2}\theta{cos}\mathrm{2}\theta{cos}\mathrm{4}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} {sin}\theta}\left({sin}\mathrm{4}\theta{cos}\mathrm{4}\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} {sin}\theta}\left({sin}\mathrm{8}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\:\frac{{sin}\left(\mathrm{7}\theta+\theta\right)}{{sin}\theta}=−\frac{\mathrm{1}}{\mathrm{8}}\:\:\:\:\:\mathrm{7}\theta=\pi \\ $$
