Question Number 164419 by akornes last updated on 16/Jan/22
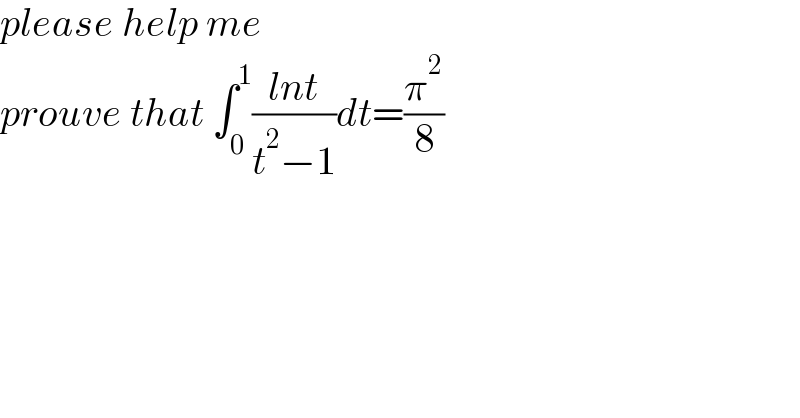
$${please}\:{help}\:{me} \\ $$$${prouve}\:{that}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnt}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Answered by Ar Brandon last updated on 17/Jan/22
![I=∫_0 ^1 ((lnt)/(t^2 −1))dt=−Σ_(n=0) ^∞ ∫_0 ^1 t^(2n) lntdt , (∵(1/(1−α))=Σ_(n=0) ^∞ α^n ) { ((u(t)=lnt)),((v′(t)=t^(2n) )) :} ⇒ { ((u′(t)=(1/t))),((v(t)=(t^(2n+1) /(2n+1)))) :} I=−Σ_(n=0) ^∞ {[(t^(2n+1) /(2n+1))lnt]_0 ^1 −(1/(2n+1))∫_0 ^1 t^(2n) dt} =Σ_(n=0) ^∞ (1/(2n+1))[(t^(2n+1) /(2n+1))]_0 ^1 =Σ_(n=0) ^∞ (1/((2n+1)^2 ))=(3/4)ζ(2)=(π^2 /8)](https://www.tinkutara.com/question/Q164443.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{t}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{n}} \mathrm{ln}{tdt}\:,\:\left(\because\frac{\mathrm{1}}{\mathrm{1}−\alpha}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\alpha^{{n}} \right) \\ $$$$\begin{cases}{{u}\left({t}\right)=\mathrm{ln}{t}}\\{{v}'\left({t}\right)={t}^{\mathrm{2}{n}} }\end{cases}\:\Rightarrow\begin{cases}{{u}'\left({t}\right)=\frac{\mathrm{1}}{{t}}}\\{{v}\left({t}\right)=\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}}\end{cases} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\left[\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\mathrm{ln}{t}\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{n}} {dt}\right\} \\ $$$$\:\:\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left[\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
