Menu Close

please-help-me-solve-these-two-questions-1-A-magician-cuts-a-rope-into-two-parts-at-a-point-selected-at-random-what-is-the-probability-that-the-length-of-the-longer-rope-is-at-least-8-times-

Tinku Tara 0 Comments
Pin




Question Number 50299 by OTCHRRE ABDULLAI last updated on 15/Dec/18
please help me solve these two questions 1. A magician cuts a rope into two parts at a point selected at random. what is the probability that the length of the longer rope is at least 8 times the length of the shorter rope. 2. find the sum of co−efficient of thebinomial expansion of (4x−1)^(16)
$${please}\:{help}\:{me}\:{solve}\:{these}\:{two} \\ $$$${questions}\: \\ $$$$\mathrm{1}.\:{A}\:{magician}\:{cuts}\:{a}\:{rope}\:{into}\:{two}\: \\ $$$$\:\:{parts}\:{at}\:{a}\:{point}\:{selected}\:{at}\: \\ $$$${random}.\:{what}\:{is}\:{the}\:{probability}\:{that} \\ $$$${the}\:{length}\:{of}\:\:{the}\:{longer}\:\:{rope}\:{is}\:{at}\:{least}\: \\ $$$$\mathrm{8}\:{times}\:{the}\:{length}\:{of}\:{the}\:{shorter}\: \\ $$$${rope}. \\ $$$$\mathrm{2}.\:{find}\:{the}\:{sum}\:{of}\:{co}−{efficient}\:{of}\: \\ $$$${thebinomial}\:\:{expansion}\:\:{of}\:\: \\ $$$$\left(\mathrm{4}{x}−\mathrm{1}\right)^{\mathrm{16}} \\ $$$$ \\ $$
Commented by OTCHRRE ABDULLAI last updated on 16/Dec/18
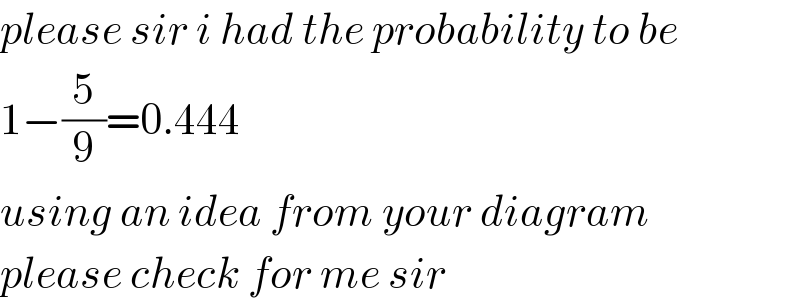
please sir i had the probability to be 1−(5/9)=0.444 using an idea from your diagram please check for me sir
$${please}\:{sir}\:{i}\:{had}\:{the}\:{probability}\:{to}\:{be}\: \\ $$$$\mathrm{1}−\frac{\mathrm{5}}{\mathrm{9}}=\mathrm{0}.\mathrm{444}\: \\ $$$${using}\:{an}\:{idea}\:{from}\:{your}\:{diagram} \\ $$$${please}\:{check}\:{for}\:{me}\:{sir} \\ $$
Commented by Abdo msup. last updated on 15/Dec/18
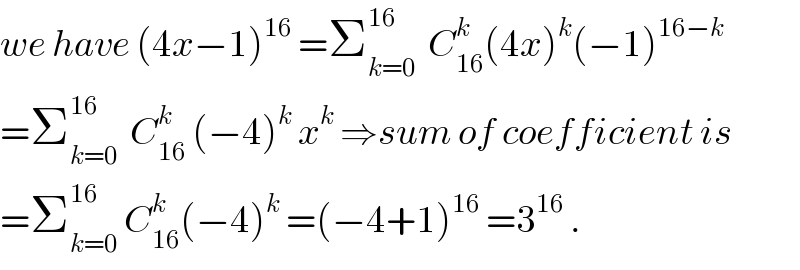
we have (4x−1)^(16) =Σ_(k=0) ^(16) C_(16) ^k (4x)^k (−1)^(16−k) =Σ_(k=0) ^(16) C_(16) ^k (−4)^k x^k ⇒sum of coefficient is =Σ_(k=0) ^(16) C_(16) ^k (−4)^k =(−4+1)^(16) =3^(16) .
$${we}\:{have}\:\left(\mathrm{4}{x}−\mathrm{1}\right)^{\mathrm{16}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \:\:{C}_{\mathrm{16}} ^{{k}} \left(\mathrm{4}{x}\right)^{{k}} \left(−\mathrm{1}\right)^{\mathrm{16}−{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \:\:{C}_{\mathrm{16}} ^{{k}} \:\left(−\mathrm{4}\right)^{{k}} \:{x}^{{k}} \:\Rightarrow{sum}\:{of}\:{coefficient}\:{is} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{16}} \:{C}_{\mathrm{16}} ^{{k}} \left(−\mathrm{4}\right)^{{k}} \:=\left(−\mathrm{4}+\mathrm{1}\right)^{\mathrm{16}} \:=\mathrm{3}^{\mathrm{16}} \:. \\ $$
Commented by mr W last updated on 16/Dec/18
to Abdullai sir: now you can also solve if the question is “what is the probability that the length of the longer rope is at least 6 times but at most 9 times of the shorter rope”. can you give it a try?
$${to}\:{Abdullai}\:{sir}: \\ $$$${now}\:{you}\:{can}\:{also}\:{solve}\:{if}\:{the}\:{question} \\ $$$${is}\:“{what}\:{is}\:{the}\:{probability}\:{that}\:{the} \\ $$$${length}\:{of}\:{the}\:{longer}\:{rope}\:{is}\:{at}\:{least} \\ $$$$\mathrm{6}\:{times}\:{but}\:{at}\:{most}\:\mathrm{9}\:{times}\:{of}\:{the} \\ $$$${shorter}\:{rope}''.\:{can}\:{you}\:{give}\:{it}\:{a}\:{try}? \\ $$
Commented by OTCHRRE ABDULLAI last updated on 16/Dec/18
Thank you very much my boss God bless you
$${Thank}\:{you}\:{very}\:{much}\:{my}\:{boss} \\ $$$${God}\:{bless}\:{you} \\ $$
Commented by OTCHRRE ABDULLAI last updated on 16/Dec/18
i will sir
$${i}\:{will}\:{sir} \\ $$
Commented by mr W last updated on 16/Dec/18
no sir! try to draw a disgram which shows the areas where the cut can be placed and then calculate the sum of these areas. the fraction of these areas is the result. the result should be (3/(35)), i think.
$${no}\:{sir}!\:{try}\:{to}\:{draw}\:{a}\:{disgram}\:{which} \\ $$$${shows}\:{the}\:{areas}\:{where}\:{the}\:{cut}\:{can}\:{be} \\ $$$${placed}\:{and}\:{then}\:{calculate}\:{the}\:{sum}\:{of} \\ $$$${these}\:{areas}.\:{the}\:{fraction}\:{of}\:{these}\:{areas} \\ $$$${is}\:{the}\:{result}. \\ $$$${the}\:{result}\:{should}\:{be}\:\frac{\mathrm{3}}{\mathrm{35}},\:{i}\:{think}. \\ $$
Commented by OTCHRRE ABDULLAI last updated on 16/Dec/18
ok sir thanks
$${ok}\:{sir}\:{thanks} \\ $$
Answered by mr W last updated on 15/Dec/18
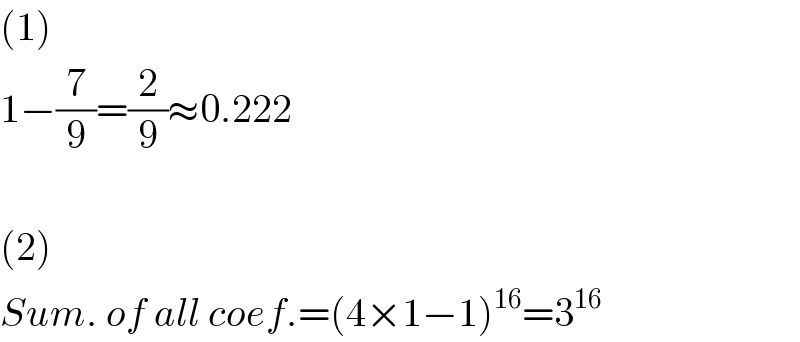
(1) 1−(7/9)=(2/9)≈0.222 (2) Sum. of all coef.=(4×1−1)^(16) =3^(16)
$$\left(\mathrm{1}\right) \\ $$$$\mathrm{1}−\frac{\mathrm{7}}{\mathrm{9}}=\frac{\mathrm{2}}{\mathrm{9}}\approx\mathrm{0}.\mathrm{222} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${Sum}.\:{of}\:{all}\:{coef}.=\left(\mathrm{4}×\mathrm{1}−\mathrm{1}\right)^{\mathrm{16}} =\mathrm{3}^{\mathrm{16}} \\ $$
Commented by mr W last updated on 15/Dec/18
Commented by OTCHRRE ABDULLAI last updated on 15/Dec/18
This man is great please can you add explanation to question 1 for me
$${This}\:{man}\:{is}\:{great} \\ $$$${please}\:{can}\:{you}\:{add}\:{explanation}\:{to}\: \\ $$$${question}\:\mathrm{1}\:{for}\:{me} \\ $$
Commented by mr W last updated on 15/Dec/18
when the cut is in the red area, the length of the longer part is less than the 8 times of the shorter part, this probability is 7/9. when the cut is in the green areas, the length of the longer part is at least 8 times of the shorter part, this probability is 1−7/9=2/9=0.222
$${when}\:{the}\:{cut}\:{is}\:{in}\:{the}\:{red}\:{area},\:{the} \\ $$$${length}\:{of}\:{the}\:{longer}\:{part}\:{is}\:{less}\:{than} \\ $$$${the}\:\mathrm{8}\:{times}\:{of}\:{the}\:{shorter}\:{part},\:{this} \\ $$$${probability}\:{is}\:\mathrm{7}/\mathrm{9}. \\ $$$${when}\:{the}\:{cut}\:{is}\:{in}\:{the}\:{green}\:{areas},\:{the} \\ $$$${length}\:{of}\:{the}\:{longer}\:{part}\:{is}\:{at}\:{least} \\ $$$$\mathrm{8}\:{times}\:{of}\:{the}\:{shorter}\:{part},\:{this} \\ $$$${probability}\:{is}\:\mathrm{1}−\mathrm{7}/\mathrm{9}=\mathrm{2}/\mathrm{9}=\mathrm{0}.\mathrm{222} \\ $$
Commented by Cheyboy last updated on 15/Dec/18
Thank alot Sir I have learn from it.
$$\mathrm{Thank}\:\mathrm{alot}\:\mathrm{Sir}\:\mathrm{I}\:\mathrm{have}\:\mathrm{learn}\:\mathrm{from}\:\mathrm{it}. \\ $$$$ \\ $$
Commented by OTCHRRE ABDULLAI last updated on 15/Dec/18
In fact mr W you are great God bless you
$${In}\:{fact}\:{mr}\:{W}\:\:{you}\:{are}\:{great}\:{God}\:{bless}\:{you} \\ $$
Commented by mr W last updated on 15/Dec/18
thanks alot sirs!
$${thanks}\:{alot}\:{sirs}! \\ $$
Commented by peter frank last updated on 15/Dec/18
yeah true he is among of best solver in this forum i real appriciate him and GOD bless him
$$\mathrm{yeah}\:\mathrm{true}\:\:\mathrm{he}\:\mathrm{is}\:\mathrm{among}\:\mathrm{of}\:\mathrm{best} \\ $$$$\mathrm{solver}\:\mathrm{in}\:\mathrm{this}\:\mathrm{forum}\:\:\mathrm{i}\:\mathrm{real}\:\mathrm{appriciate}\:\mathrm{him}\:\mathrm{and}\:\mathrm{GOD}\:\mathrm{bless}\:\mathrm{him} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *