Question Number 170545 by kndramaths last updated on 26/May/22
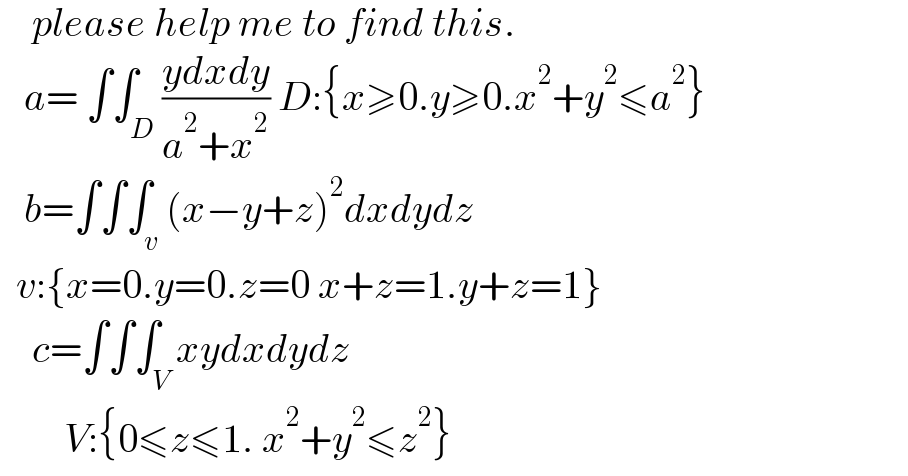
$$\:\:\:\:{please}\:{help}\:{me}\:{to}\:{find}\:{this}. \\ $$$$\:\:\:{a}=\:\int\int_{{D}} \frac{{ydxdy}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{D}:\left\{{x}\geqslant\mathrm{0}.{y}\geqslant\mathrm{0}.{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \right\} \\ $$$$\:\:\:{b}=\int\int\int_{{v}} \left({x}−{y}+{z}\right)^{\mathrm{2}} {dxdydz} \\ $$$$\:\:{v}:\left\{{x}=\mathrm{0}.{y}=\mathrm{0}.{z}=\mathrm{0}\:{x}+{z}=\mathrm{1}.{y}+{z}=\mathrm{1}\right\} \\ $$$$\:\:\:\:{c}=\int\int\int_{{V}} {xydxdydz} \\ $$$$\:\:\:\:\:\:\:\:{V}:\left\{\mathrm{0}\leqslant{z}\leqslant\mathrm{1}.\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant{z}^{\mathrm{2}} \right\} \\ $$
Commented by kndramaths last updated on 27/May/22
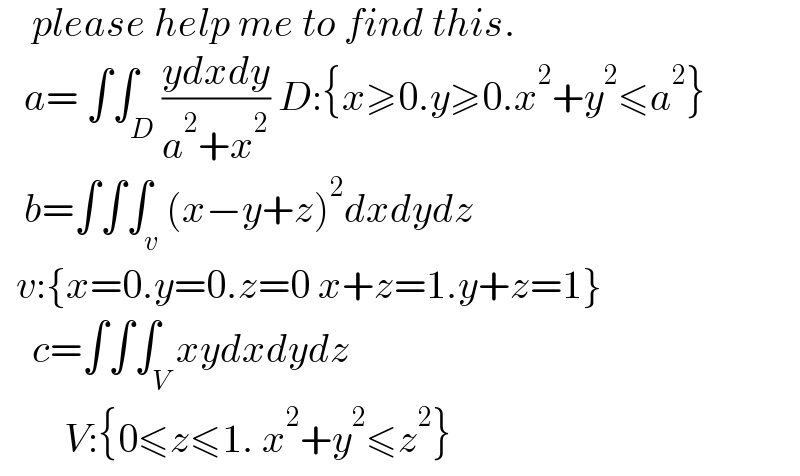
$$\:\:\:\:{please}\:{help}\:{me}\:{to}\:{find}\:{this}. \\ $$$$\:\:\:{a}=\:\int\int_{{D}} \frac{{ydxdy}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{D}:\left\{{x}\geqslant\mathrm{0}.{y}\geqslant\mathrm{0}.{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \right\} \\ $$$$\:\:\:{b}=\int\int\int_{{v}} \left({x}−{y}+{z}\right)^{\mathrm{2}} {dxdydz} \\ $$$$\:\:{v}:\left\{{x}=\mathrm{0}.{y}=\mathrm{0}.{z}=\mathrm{0}\:{x}+{z}=\mathrm{1}.{y}+{z}=\mathrm{1}\right\} \\ $$$$\:\:\:\:{c}=\int\int\int_{{V}} {xydxdydz} \\ $$$$\:\:\:\:\:\:\:\:{V}:\left\{\mathrm{0}\leqslant{z}\leqslant\mathrm{1}.\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant{z}^{\mathrm{2}} \right\} \\ $$
