please-help-me-y-9-x-2-Q-find-domain-and-range-of-given-real-function-i-found-the-domain-3-3-but-for-range-i-followed-this-way-y-2-9-x-2-x-2-9-y-2-x-9-y-2-y-3-3-but-the-answer-i

Question Number 52610 by Kunal12588 last updated on 10/Jan/19

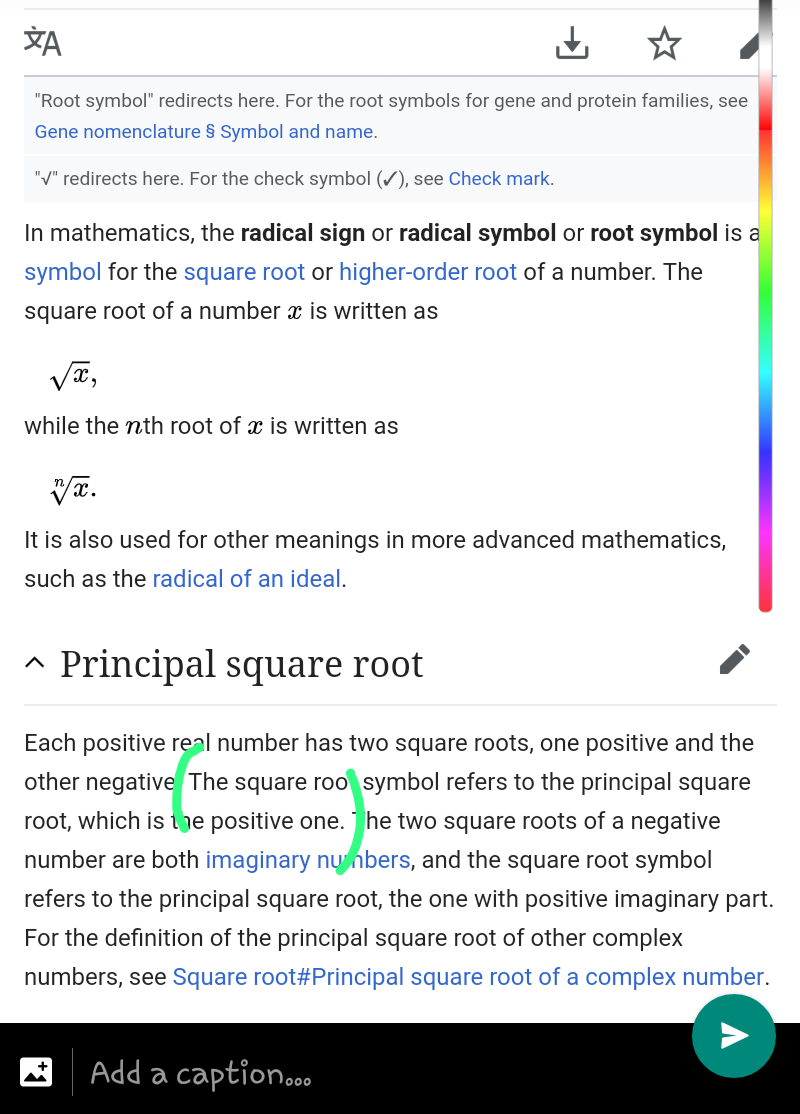
p l e a s e h e l p m e

y = \sqrt{9 - x^{2}}

Q f i n d d o m a i n a n d r a n g e o f g i v e n r e a l f u n c t i o n

i f o u n d t h e d o m a i n = [- 3, 3]

b u t f o r r a n g e i f o l l o w e d t h i s w a y

y^{2} = 9 - x^{2}

x^{2} = 9 - y^{2} \Rightarrow x = \sqrt{9 - y^{2}} \Rightarrow y = [- 3, 3]

b u t t h e a n s w e r i s [0, 3]

a f t e r c h e c k i n g t h e g r a p h y ⩾ 0 . y e s i t s t r u e

w e h a v e t o t a k e p o s i t i v e r o o t b u t h o w c a n i

w r i t e i t

Commented by Kunal12588 last updated on 10/Jan/19

o f f c o u r s e s i r b u t t o m m o r o w i s m y t e s t i {c a n}^{'} t

d r a w g r a p h s t h e i r

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

t o m y v i e w i t i s b e t t e r t o c o s u l t s g r a p h \dots a v a i l a b l e

i n p l a y s t o r e \dots s o m e q u e s t i o n s e a s i l y u n d e r s t o o d

f r o m g r a p h \dots

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Jan/19

Commented by Kunal12588 last updated on 10/Jan/19

t h a n k y o u s i r

Answered by kaivan.ahmadi last updated on 10/Jan/19

since y = \sqrt{9 - x^{2}} so y ⩾ 0 . it means \min (y) = 0

and found \max (y)

y is \max when 9 - x^{2} is \max

so \max (y) = \sqrt{9} = 3

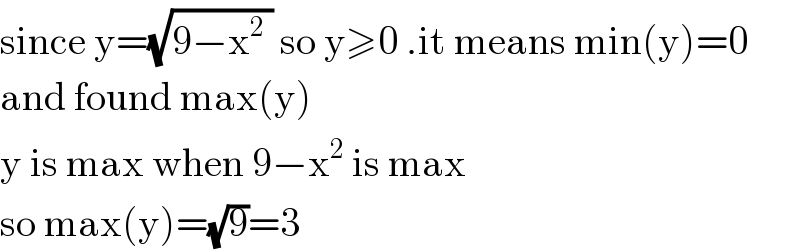
Commented by Kunal12588 last updated on 10/Jan/19

t h a n k y o u s i r