Question Number 96604 by Rio Michael last updated on 03/Jun/20

$$\mathrm{Please}\:\mathrm{how}\:\mathrm{will}\:\mathrm{you}\:\mathrm{evaluate} \\ $$$$\:\int\:\sqrt{{dx}}\:??? \\ $$
Commented by MJS last updated on 03/Jun/20

$$\mathrm{it}'\mathrm{s}\:\mathrm{an}\:\mathrm{error}\:\mathrm{of}\:\mathrm{syntax}.\:“{dx}''\:\mathrm{has}\:\mathrm{to}\:\mathrm{be}\:\mathrm{the}\:\mathrm{last} \\ $$$$\mathrm{term}\:\mathrm{of}\:\mathrm{an}\:\mathrm{integral}.\:“{dx}''\:\mathrm{can}\:\mathrm{never}\:\mathrm{be}\:\mathrm{a} \\ $$$$\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{term}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{integrate}. \\ $$$$\int{dx}\:\mathrm{is}\:\mathrm{a}\:\mathrm{short}\:\mathrm{cut}\:\mathrm{for}\:\int\mathrm{1}{dx};\:\int\frac{{dx}}{…}\:\mathrm{is}\:\mathrm{short} \\ $$$$\mathrm{for}\:\int\frac{\mathrm{1}}{…}{dx} \\ $$$$\mathrm{but} \\ $$$$\int\frac{…}{{dx}};\:\underset{{dx}} {\int}…;\:\int{dx}^{{n}} ;\:\mathrm{generally}\:\int{f}\left({dx}\right)\:\mathrm{are}\:\mathrm{all} \\ $$$$\mathrm{meaningless} \\ $$
Commented by prakash jain last updated on 03/Jun/20
Hi Rio,
for fraction derivative study you can begin by reading wikipedia article
https://en.m.wikipedia.org/wiki/Fractional_calculus
Commented by prakash jain last updated on 03/Jun/20
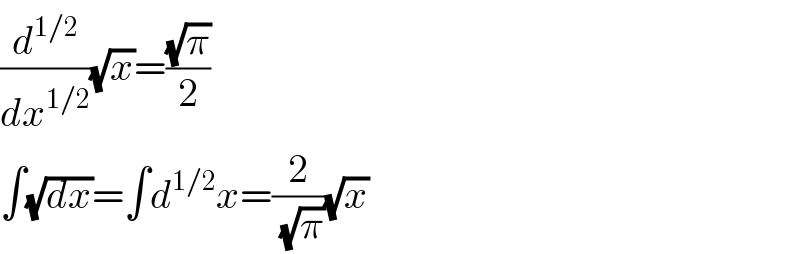
$$\frac{{d}^{\mathrm{1}/\mathrm{2}} }{{dx}^{\mathrm{1}/\mathrm{2}} }\sqrt{{x}}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\int\sqrt{{dx}}=\int{d}^{\mathrm{1}/\mathrm{2}} {x}=\frac{\mathrm{2}}{\:\sqrt{\pi}}\sqrt{{x}} \\ $$
Commented by MJS last updated on 03/Jun/20

$$\mathrm{I}\:\mathrm{know}\:\mathrm{about}\:\mathrm{fractional}\:\mathrm{derivates}\:\mathrm{and} \\ $$$$\mathrm{integrals}\:\mathrm{but}\:\mathrm{I}\:\mathrm{think}\:\mathrm{most}\:\mathrm{of}\:\mathrm{these}\:\mathrm{questions} \\ $$$$\mathrm{in}\:\mathrm{here}\:\mathrm{are}\:\mathrm{rather}\:\mathrm{typos} \\ $$
Commented by Rio Michael last updated on 03/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{will}\:\mathrm{check}\:\mathrm{it}\:\mathrm{out}. \\ $$
Commented by Rio Michael last updated on 03/Jun/20

$$\mathrm{Sir}\:\mathrm{i}\:\mathrm{think}\:\mathrm{there}'\mathrm{s}\:\:\mathrm{just}\:\mathrm{some}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{it},\:\mathrm{just}\:\mathrm{some}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}..\mathrm{an}\:\mathrm{i}'\mathrm{m}\:\mathrm{guessing} \\ $$$$\mathrm{fractional}\:\mathrm{integral}\:\mathrm{should}\:\mathrm{work}. \\ $$
