Menu Close

please-i-need-cubic-formula-

Tinku Tara 0 Comments
Pin




Question Number 171829 by Mikenice last updated on 21/Jun/22
please i need cubic formula
$${please}\:{i}\:{need}\:{cubic}\:{formula} \\ $$$$ \\ $$
Answered by MathematicalUser2357 last updated on 05/Jan/24
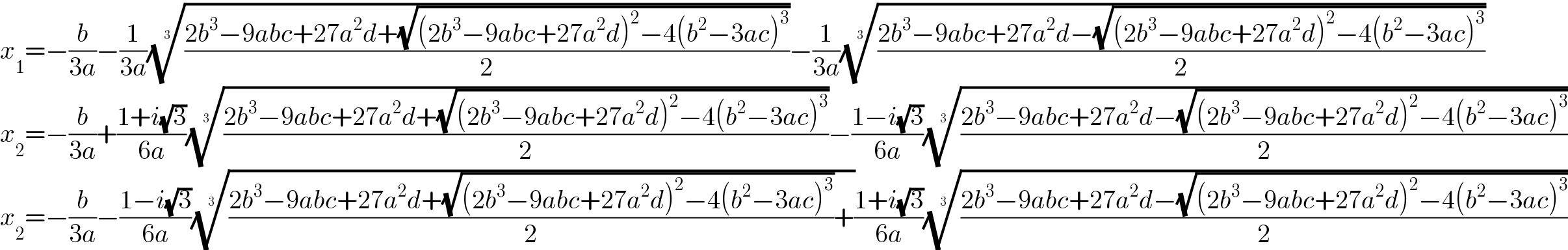
x_1 =−(b/(3a))−(1/(3a))(((2b^3 −9abc+27a^2 d+(√((2b^3 −9abc+27a^2 d)^2 −4(b^2 −3ac)^3 )))/2))^(1/3) −(1/(3a))(((2b^3 −9abc+27a^2 d−(√((2b^3 −9abc+27a^2 d)^2 −4(b^2 −3ac)^3 )))/2))^(1/3) x_2 =−(b/(3a))+((1+i(√3))/(6a))(((2b^3 −9abc+27a^2 d+(√((2b^3 −9abc+27a^2 d)^2 −4(b^2 −3ac)^3 )))/2))^(1/3) −((1−i(√3))/(6a))(((2b^3 −9abc+27a^2 d−(√((2b^3 −9abc+27a^2 d)^2 −4(b^2 −3ac)^3 )))/2))^(1/3) x_2 =−(b/(3a))−((1−i(√3))/(6a))((((2b^3 −9abc+27a^2 d+(√((2b^3 −9abc+27a^2 d)^2 −4(b^2 −3ac)^3 )))/2)+))^(1/3) ((1+i(√3))/(6a))(((2b^3 −9abc+27a^2 d−(√((2b^3 −9abc+27a^2 d)^2 −4(b^2 −3ac)^3 )))/2))^(1/3)
$${x}_{\mathrm{1}} =−\frac{{b}}{\mathrm{3}{a}}−\frac{\mathrm{1}}{\mathrm{3}{a}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}+\sqrt{\left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{3}{ac}\right)^{\mathrm{3}} }}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{3}{a}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}−\sqrt{\left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{3}{ac}\right)^{\mathrm{3}} }}{\mathrm{2}}} \\ $$$${x}_{\mathrm{2}} =−\frac{{b}}{\mathrm{3}{a}}+\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{6}{a}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}+\sqrt{\left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{3}{ac}\right)^{\mathrm{3}} }}{\mathrm{2}}}−\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{6}{a}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}−\sqrt{\left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{3}{ac}\right)^{\mathrm{3}} }}{\mathrm{2}}} \\ $$$${x}_{\mathrm{2}} =−\frac{{b}}{\mathrm{3}{a}}−\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{6}{a}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}+\sqrt{\left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{3}{ac}\right)^{\mathrm{3}} }}{\mathrm{2}}+}\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{6}{a}}\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}−\sqrt{\left(\mathrm{2}{b}^{\mathrm{3}} −\mathrm{9}{abc}+\mathrm{27}{a}^{\mathrm{2}} {d}\right)^{\mathrm{2}} −\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{3}{ac}\right)^{\mathrm{3}} }}{\mathrm{2}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *