please-I-need-help-e-x-1-e-2x-1-dx-

Question Number 130226 by stelor last updated on 23/Jan/21

$$\mathrm{please}\:\mathrm{I}\:\mathrm{need}\:\mathrm{help}… \\ $$$$\int\left(\frac{\mathrm{e}^{{x}} +\mathrm{1}}{\mathrm{e}^{\mathrm{2x}} +\mathrm{1}}\right){dx} \\ $$

Answered by Lordose last updated on 23/Jan/21

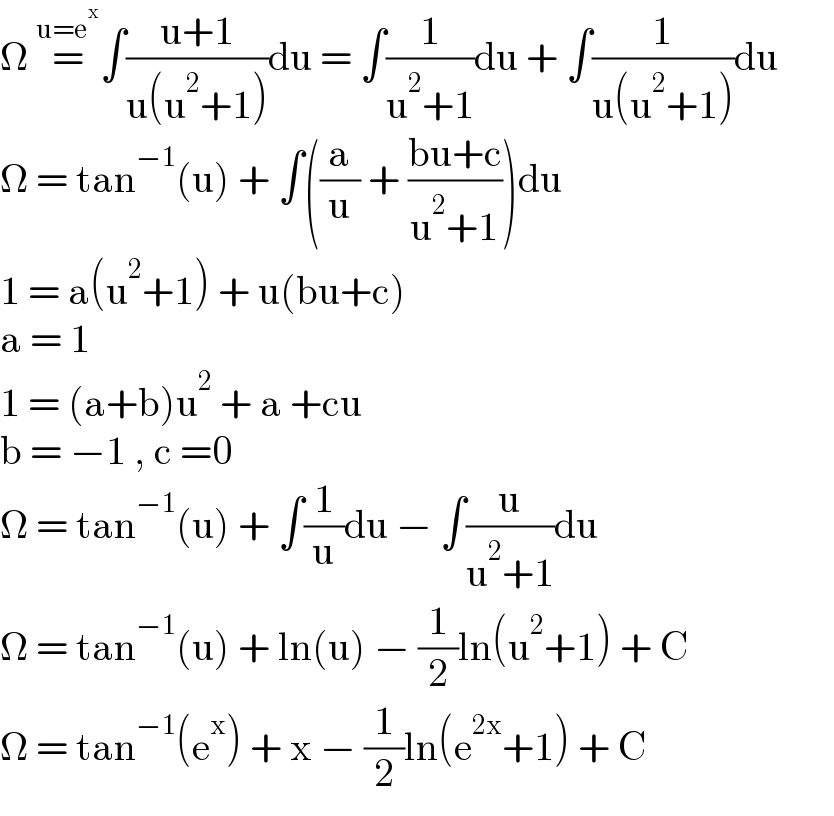
Ω =^(u=e^x ) ∫((u+1)/(u(u^2 +1)))du = ∫(1/(u^2 +1))du + ∫(1/(u(u^2 +1)))du Ω = tan^(−1) (u) + ∫((a/u) + ((bu+c)/(u^2 +1)))du 1 = a(u^2 +1) + u(bu+c) a = 1 1 = (a+b)u^2 + a +cu b = −1 , c =0 Ω = tan^(−1) (u) + ∫(1/u)du − ∫(u/(u^2 +1))du Ω = tan^(−1) (u) + ln(u) − (1/2)ln(u^2 +1) + C Ω = tan^(−1) (e^x ) + x − (1/2)ln(e^(2x) +1) + C

$$\Omega\:\overset{\mathrm{u}=\mathrm{e}^{\mathrm{x}} } {=}\int\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{du}\:=\:\int\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\mathrm{du}\:+\:\int\frac{\mathrm{1}}{\mathrm{u}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{du}\:\:\:\:\:\:\: \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\:+\:\int\left(\frac{\mathrm{a}}{\mathrm{u}}\:+\:\frac{\mathrm{bu}+\mathrm{c}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{du} \\ $$$$\mathrm{1}\:=\:\mathrm{a}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)\:+\:\mathrm{u}\left(\mathrm{bu}+\mathrm{c}\right) \\ $$$$\mathrm{a}\:=\:\mathrm{1} \\ $$$$\mathrm{1}\:=\:\left(\mathrm{a}+\mathrm{b}\right)\mathrm{u}^{\mathrm{2}} \:+\:\mathrm{a}\:+\mathrm{cu} \\ $$$$\mathrm{b}\:=\:−\mathrm{1}\:,\:\mathrm{c}\:=\mathrm{0} \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\:+\:\int\frac{\mathrm{1}}{\mathrm{u}}\mathrm{du}\:−\:\int\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\mathrm{du} \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\:+\:\mathrm{ln}\left(\mathrm{u}\right)\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)\:+\:\mathrm{C} \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)\:+\:\mathrm{x}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{e}^{\mathrm{2x}} +\mathrm{1}\right)\:+\:\mathrm{C} \\ $$

Commented by stelor last updated on 23/Jan/21

$$\mathrm{good}…… \\ $$

Answered by EDWIN88 last updated on 23/Jan/21

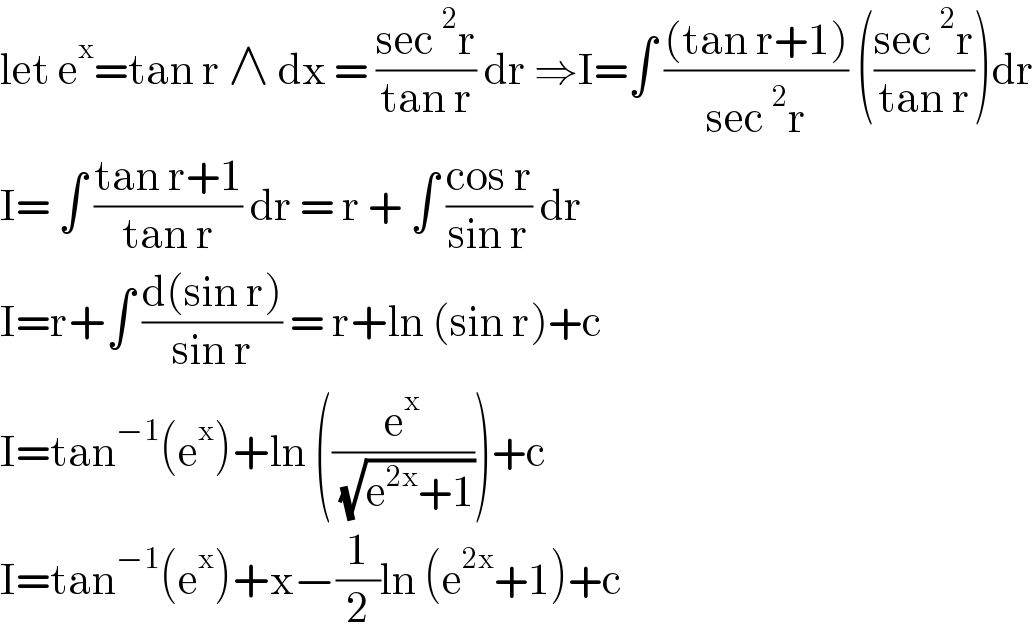
let e^x =tan r ∧ dx = ((sec^2 r)/(tan r)) dr ⇒I=∫ (((tan r+1))/(sec^2 r)) (((sec^2 r)/(tan r)))dr I= ∫ ((tan r+1)/(tan r)) dr = r + ∫ ((cos r)/(sin r)) dr I=r+∫ ((d(sin r))/(sin r)) = r+ln (sin r)+c I=tan^(−1) (e^x )+ln ((e^x /( (√(e^(2x) +1)))))+c I=tan^(−1) (e^x )+x−(1/2)ln (e^(2x) +1)+c

$$\mathrm{let}\:\mathrm{e}^{\mathrm{x}} =\mathrm{tan}\:\mathrm{r}\:\wedge\:\mathrm{dx}\:=\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{r}}{\mathrm{tan}\:\mathrm{r}}\:\mathrm{dr}\:\Rightarrow\mathrm{I}=\int\:\frac{\left(\mathrm{tan}\:\mathrm{r}+\mathrm{1}\right)}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{r}}\:\left(\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{r}}{\mathrm{tan}\:\mathrm{r}}\right)\mathrm{dr} \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{tan}\:\mathrm{r}+\mathrm{1}}{\mathrm{tan}\:\mathrm{r}}\:\mathrm{dr}\:=\:\mathrm{r}\:+\:\int\:\frac{\mathrm{cos}\:\mathrm{r}}{\mathrm{sin}\:\mathrm{r}}\:\mathrm{dr} \\ $$$$\mathrm{I}=\mathrm{r}+\int\:\frac{\mathrm{d}\left(\mathrm{sin}\:\mathrm{r}\right)}{\mathrm{sin}\:\mathrm{r}}\:=\:\mathrm{r}+\mathrm{ln}\:\left(\mathrm{sin}\:\mathrm{r}\right)+\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{ln}\:\left(\frac{\mathrm{e}^{\mathrm{x}} }{\:\sqrt{\mathrm{e}^{\mathrm{2x}} +\mathrm{1}}}\right)+\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{2x}} +\mathrm{1}\right)+\mathrm{c} \\ $$

Commented by bramlexs22 last updated on 23/Jan/21

$$\mathrm{waw}…\mathrm{elegant} \\ $$

Commented by stelor last updated on 23/Jan/21

$$\mathrm{cool}… \\ $$

Facebook Tweet Pin

please-I-need-help-e-x-1-e-2x-1-dx-

Leave a Reply Cancel reply