Question Number 33410 by NECx last updated on 15/Apr/18

$${please}\:{is}\:{there}\:{any}\:{general}\:{way}\:{for} \\ $$$${calculating}\:{the}\:{error}\:{or}\:{uncertainty} \\ $$$${in}\:{g}\:{when} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:{m}=\frac{\mathrm{4}\pi^{\mathrm{2}} }{{g}}\:{where}\:{m}={slope}\:{and} \\ $$$${g}={acceleration}\:{due}\:{to}\:{gravity} \\ $$$$ \\ $$$$ \\ $$$${please}\:{help} \\ $$
Commented by Rio Mike last updated on 15/Apr/18
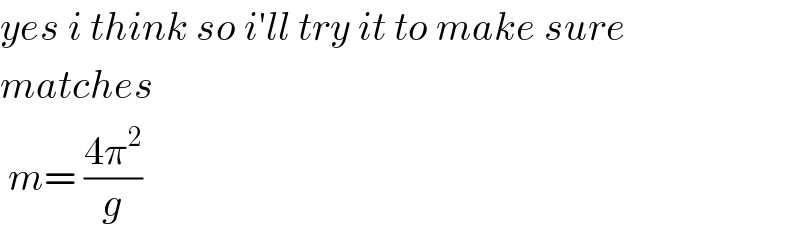
$${yes}\:{i}\:{think}\:{so}\:{i}'{ll}\:{try}\:{it}\:{to}\:{make}\:{sure} \\ $$$${matches} \\ $$$$\:{m}=\:\frac{\mathrm{4}\pi^{\mathrm{2}} }{{g}} \\ $$
Answered by MJS last updated on 15/Apr/18
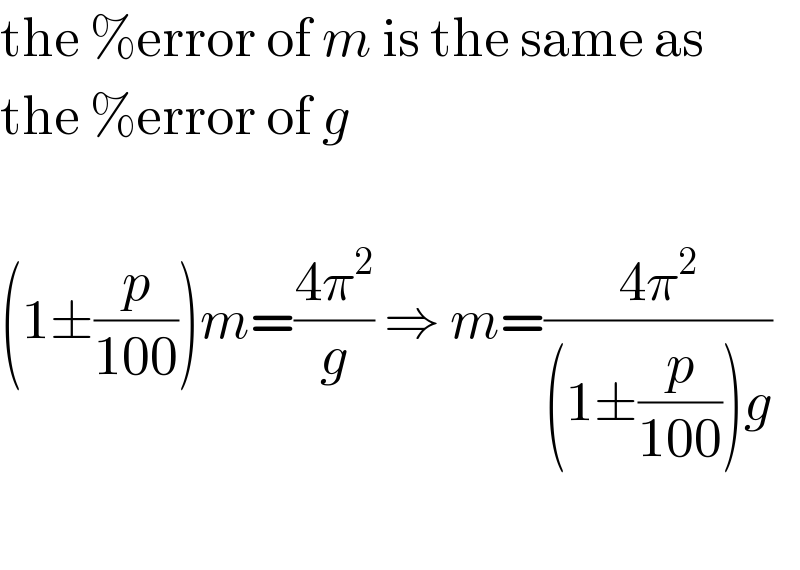
$$\mathrm{the}\:\%\mathrm{error}\:\mathrm{of}\:{m}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as} \\ $$$$\mathrm{the}\:\%\mathrm{error}\:\mathrm{of}\:{g} \\ $$$$ \\ $$$$\left(\mathrm{1}\pm\frac{{p}}{\mathrm{100}}\right){m}=\frac{\mathrm{4}\pi^{\mathrm{2}} }{{g}}\:\Rightarrow\:{m}=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\left(\mathrm{1}\pm\frac{{p}}{\mathrm{100}}\right){g}} \\ $$$$ \\ $$
Commented by NECx last updated on 16/Apr/18
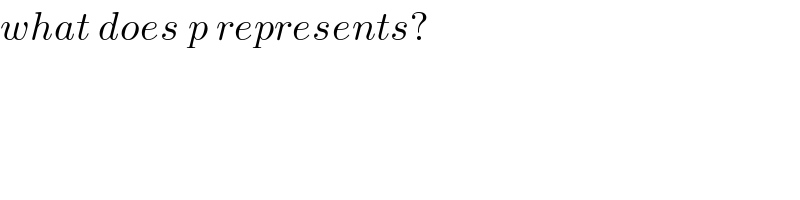
$${what}\:{does}\:{p}\:{represents}? \\ $$
Commented by MJS last updated on 16/Apr/18
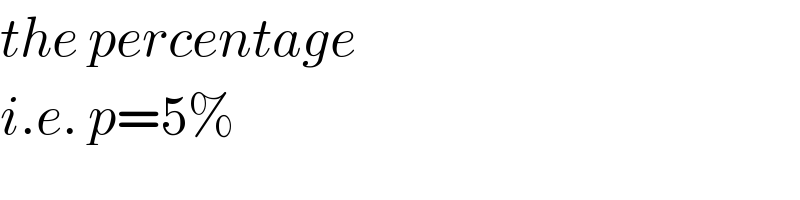
$${the}\:{percentage} \\ $$$${i}.{e}.\:{p}=\mathrm{5\%} \\ $$
