Question Number 108738 by mnjuly1970 last updated on 19/Aug/20
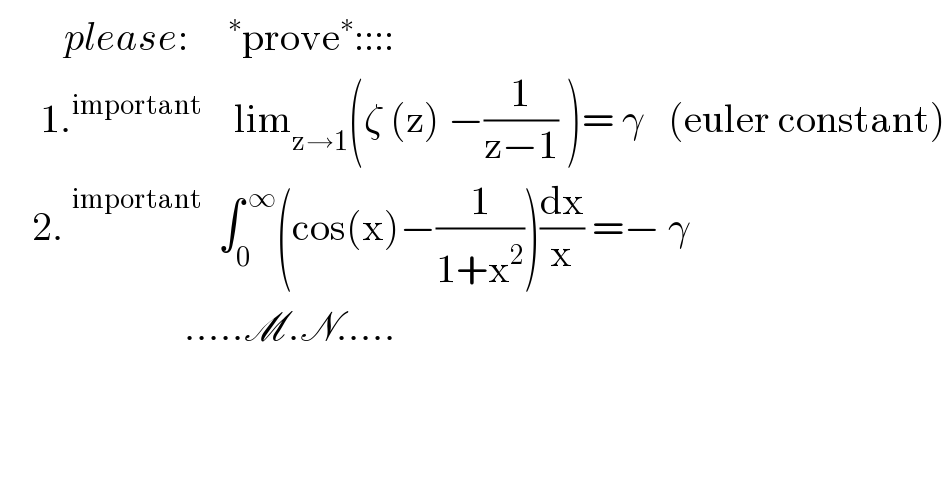
$$\:\:\:\:\:\:\:\:{please}:\:\:\:\:\:^{\ast} \mathrm{prove}^{\ast} :::: \\ $$$$\:\:\:\:\:\mathrm{1}.^{\mathrm{important}} \:\:\:\:\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \left(\zeta\:\left(\mathrm{z}\right)\:−\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}\:\right)=\:\gamma\:\:\:\left(\mathrm{euler}\:\mathrm{constant}\right) \\ $$$$\:\:\:\:\mathrm{2}.\:\overset{\mathrm{important}} {\:}\:\:\int_{\mathrm{0}} ^{\:\infty} \left(\mathrm{cos}\left(\mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\frac{\mathrm{dx}}{\mathrm{x}}\:=−\:\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\mathscr{M}.\mathscr{N}….. \\ $$$$\: \\ $$
