Question Number 97490 by ali_golmakani last updated on 08/Jun/20
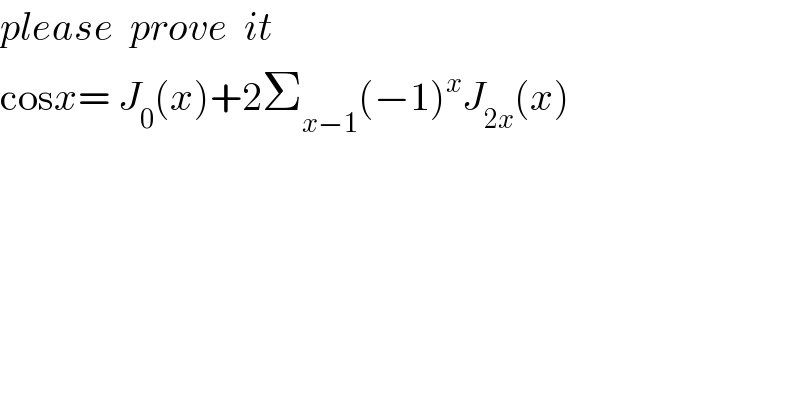
$${please}\:\:{prove}\:\:{it} \\ $$$$\mathrm{cos}{x}=\:{J}_{\mathrm{0}} \left({x}\right)+\mathrm{2}\sum_{{x}−\mathrm{1}} \left(−\mathrm{1}\right)^{{x}} {J}_{\mathrm{2}{x}} \left({x}\right) \\ $$
Answered by smridha last updated on 08/Jun/20

$$\boldsymbol{{I}}\:\boldsymbol{{think}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{needed}}\:\boldsymbol{{to}}\:\boldsymbol{{check}}\:\boldsymbol{{your}} \\ $$$$\boldsymbol{{question}} \\ $$$$\sum_{\boldsymbol{{x}}−\mathrm{1}} \left(−\mathrm{1}\right)^{\boldsymbol{{x}}} \boldsymbol{{J}}_{\mathrm{2}{x}} \left({x}\right)\:\boldsymbol{{what}}\:\boldsymbol{{does}}\:\boldsymbol{{it}}\:\boldsymbol{{mean}}? \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{think}}\:\boldsymbol{{J}}_{\mathrm{2}\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)\:\boldsymbol{{B}}{essel}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} . \\ $$
Commented by ali_golmakani last updated on 08/Jun/20

$${yes} \\ $$
