Question Number 161559 by stelor last updated on 19/Dec/21
![please show that (1/2) + cosx + cos2x + cos3x + ... + cosnx = ((sin[(n+1)(x/2)])/(2sin(x/2)))](https://www.tinkutara.com/question/Q161559.png)
$${please}\:{show}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:{cosx}\:+\:{cos}\mathrm{2}{x}\:+\:{cos}\mathrm{3}{x}\:+\:…\:+\:{cosnx}\:=\:\frac{{sin}\left[\left({n}+\mathrm{1}\right)\frac{{x}}{\mathrm{2}}\right]}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$
Answered by Ar Brandon last updated on 19/Dec/21
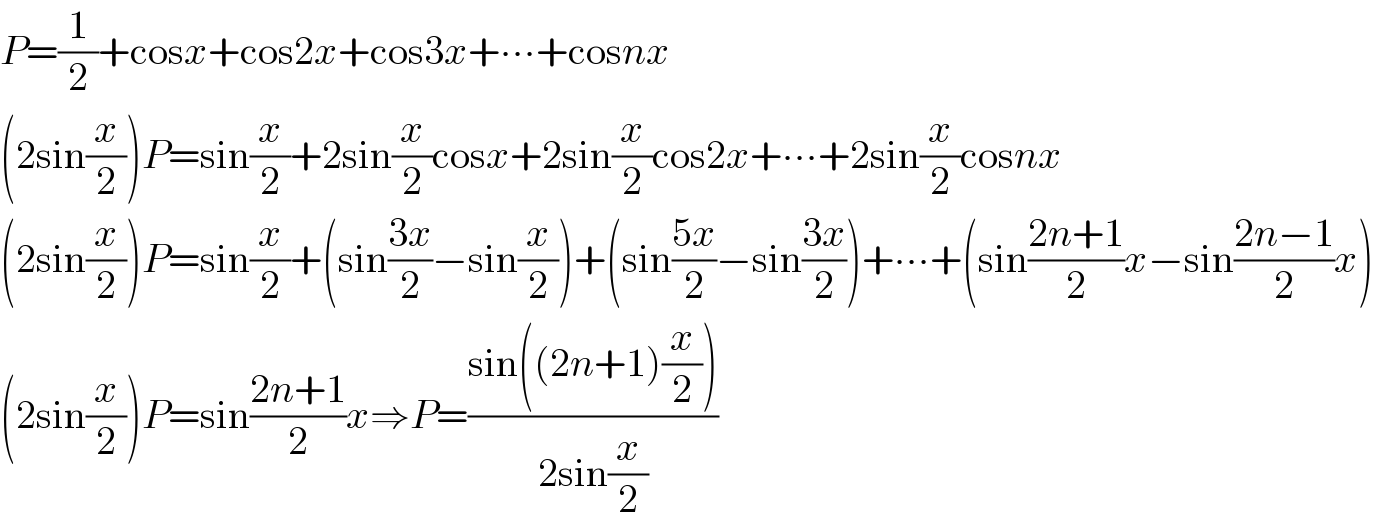
$${P}=\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}{x}+\mathrm{cos2}{x}+\mathrm{cos3}{x}+\centerdot\centerdot\centerdot+\mathrm{cos}{nx} \\ $$$$\left(\mathrm{2sin}\frac{{x}}{\mathrm{2}}\right){P}=\mathrm{sin}\frac{{x}}{\mathrm{2}}+\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}{x}+\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos2}{x}+\centerdot\centerdot\centerdot+\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}{nx} \\ $$$$\left(\mathrm{2sin}\frac{{x}}{\mathrm{2}}\right){P}=\mathrm{sin}\frac{{x}}{\mathrm{2}}+\left(\mathrm{sin}\frac{\mathrm{3}{x}}{\mathrm{2}}−\mathrm{sin}\frac{{x}}{\mathrm{2}}\right)+\left(\mathrm{sin}\frac{\mathrm{5}{x}}{\mathrm{2}}−\mathrm{sin}\frac{\mathrm{3}{x}}{\mathrm{2}}\right)+\centerdot\centerdot\centerdot+\left(\mathrm{sin}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}{x}−\mathrm{sin}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}{x}\right) \\ $$$$\left(\mathrm{2sin}\frac{{x}}{\mathrm{2}}\right){P}=\mathrm{sin}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}{x}\Rightarrow{P}=\frac{\mathrm{sin}\left(\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2sin}\frac{{x}}{\mathrm{2}}} \\ $$
Commented by stelor last updated on 19/Dec/21

$${thanks}. \\ $$
