Question Number 174804 by Kallu last updated on 11/Aug/22
$${Please}\:{solve}\:. \\ $$
Commented by Kallu last updated on 11/Aug/22
Commented by ajfour last updated on 12/Aug/22
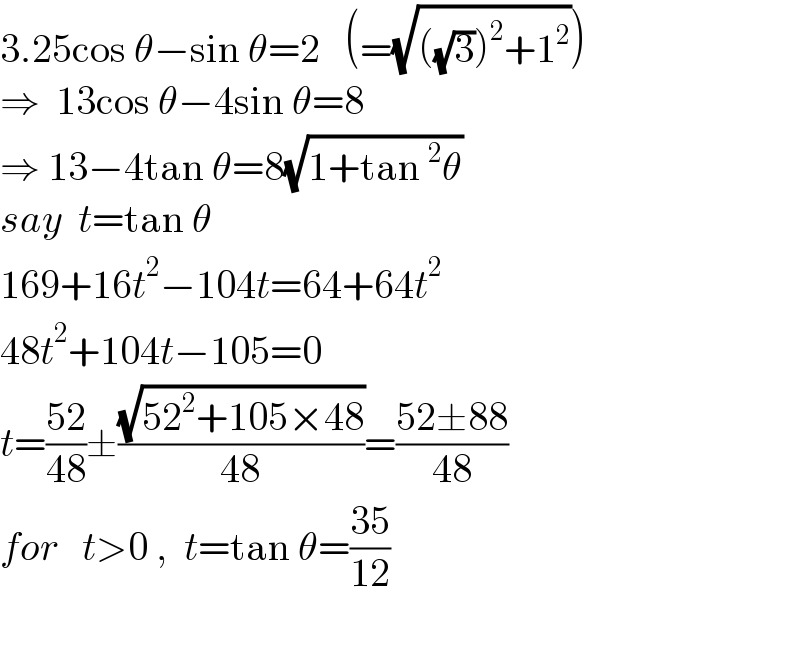
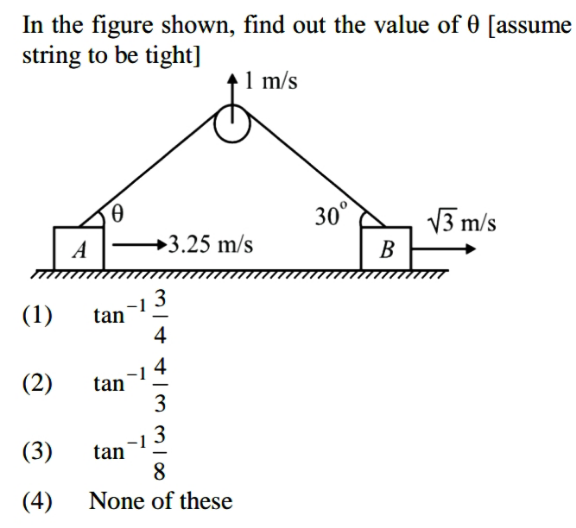
$$\mathrm{3}.\mathrm{25cos}\:\theta−\mathrm{sin}\:\theta=\mathrm{2}\:\:\:\left(=\sqrt{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:\mathrm{13cos}\:\theta−\mathrm{4sin}\:\theta=\mathrm{8} \\ $$$$\Rightarrow\:\mathrm{13}−\mathrm{4tan}\:\theta=\mathrm{8}\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$${say}\:\:{t}=\mathrm{tan}\:\theta \\ $$$$\mathrm{169}+\mathrm{16}{t}^{\mathrm{2}} −\mathrm{104}{t}=\mathrm{64}+\mathrm{64}{t}^{\mathrm{2}} \\ $$$$\mathrm{48}{t}^{\mathrm{2}} +\mathrm{104}{t}−\mathrm{105}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{52}}{\mathrm{48}}\pm\frac{\sqrt{\mathrm{52}^{\mathrm{2}} +\mathrm{105}×\mathrm{48}}}{\mathrm{48}}=\frac{\mathrm{52}\pm\mathrm{88}}{\mathrm{48}} \\ $$$${for}\:\:\:{t}>\mathrm{0}\:,\:\:{t}=\mathrm{tan}\:\theta=\frac{\mathrm{35}}{\mathrm{12}} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 12/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Kallu last updated on 12/Aug/22

$${The}\:{correct}\:{answer}\:{is}\:{option}\:{A}\: \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$
