Menu Close

please-solve-0-pi-4-tan-9-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 116196 by mnjuly1970 last updated on 01/Oct/20
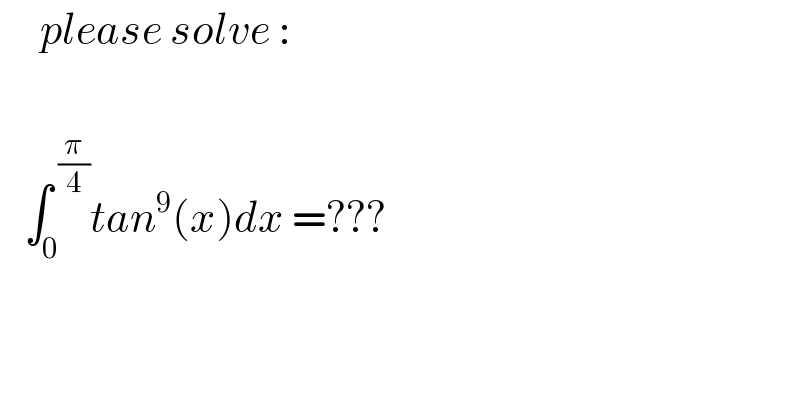
please solve : ∫_0 ^( (π/4)) tan^9 (x)dx =???
$$\:\:\:\:\:{please}\:{solve}\:: \\ $$$$\:\:\: \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {tan}^{\mathrm{9}} \left({x}\right){dx}\:=??? \\ $$
Answered by mindispower last updated on 01/Oct/20
let u_n =∫_0 ^(π/4) tg^n (x)dx U_(n+2) +U_n =∫_0 ^(π/4) tg^n (x)dx+∫_0 ^(π/4) tg^(n+2) (x)dx =∫_0 ^(π/4) tg^n (x)(1+tg^2 (x))dx=∫_0 ^(π/4) tg^n (x)d(tg(x)) =[((tg^(n+1) (x))/(n+1))]_0 ^(π/4) =(1/(n+1)) ⇒U_(n+2) =(1/(n+1))−U_n U_0 =(π/4),U_1 =∫_0 ^(π/4) tg(x)dx=[−ln(cos(x))]_0 ^(π/4) =ln((√2)) U_3 =−U_1 +(1/2) U_5 =−U_3 +(1/4) U_7 =−U_5 +(1/6) U_9 =−U_7 +(1/8) =(1/8)−(1/6)+(1/4)−(1/2)+ln((√2)) =((3−4+6−12)/(24))+ln((√2)) =((−7+12ln(2))/(24))
$${let} \\ $$$${u}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}^{{n}} \left({x}\right){dx} \\ $$$${U}_{{n}+\mathrm{2}} +{U}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}^{{n}} \left({x}\right){dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}^{{n}+\mathrm{2}} \left({x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}^{{n}} \left({x}\right)\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}^{{n}} \left({x}\right){d}\left({tg}\left({x}\right)\right) \\ $$$$=\left[\frac{{tg}^{{n}+\mathrm{1}} \left({x}\right)}{{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\Rightarrow{U}_{{n}+\mathrm{2}} =\frac{\mathrm{1}}{{n}+\mathrm{1}}−{U}_{{n}} \\ $$$${U}_{\mathrm{0}} =\frac{\pi}{\mathrm{4}},{U}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}\left({x}\right){dx}=\left[−{ln}\left({cos}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$={ln}\left(\sqrt{\mathrm{2}}\right) \\ $$$${U}_{\mathrm{3}} =−{U}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${U}_{\mathrm{5}} =−{U}_{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${U}_{\mathrm{7}} =−{U}_{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${U}_{\mathrm{9}} =−{U}_{\mathrm{7}} +\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}+{ln}\left(\sqrt{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}−\mathrm{4}+\mathrm{6}−\mathrm{12}}{\mathrm{24}}+{ln}\left(\sqrt{\mathrm{2}}\right) \\ $$$$=\frac{−\mathrm{7}+\mathrm{12}{ln}\left(\mathrm{2}\right)}{\mathrm{24}} \\ $$
Commented by mnjuly1970 last updated on 01/Oct/20
thank you sir..
$${thank}\:{you}\:{sir}.. \\ $$
Answered by MJS_new last updated on 01/Oct/20
∫tan^9 x dx= [t=tan x → dx=(dt/(t^2 +1))] =∫(t^9 /(t^2 +1))dt=∫((t/(t^2 +1))+t^7 −t^5 +t^3 −t)dt= =(1/2)ln (t^2 +1) +(t^8 /8)−(t^6 /6)+(t^4 /4)−(t^2 /2) ⇒ answer is (1/2)ln 2 −(7/(24))
$$\int\mathrm{tan}^{\mathrm{9}} \:{x}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{t}^{\mathrm{9}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\int\left(\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+{t}^{\mathrm{7}} −{t}^{\mathrm{5}} +{t}^{\mathrm{3}} −{t}\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{{t}^{\mathrm{8}} }{\mathrm{8}}−\frac{{t}^{\mathrm{6}} }{\mathrm{6}}+\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2}\:−\frac{\mathrm{7}}{\mathrm{24}} \\ $$
Commented by mnjuly1970 last updated on 01/Oct/20
grateful..
$${grateful}.. \\ $$
Answered by mathmax by abdo last updated on 01/Oct/20
let u_n =∫_0 ^(π/4) tan^(2n+1) xdx ⇒u_n =∫_0 ^(π/4) tan^(2n−1) x(1+ tan^2 x−1) dx =∫_0 ^(π/4) tan^(2n−1) (1+tan^2 x)dx−u_(n−1) we hsve ∫_0 ^(π/4) (1+tan^2 x)^(2n−1) dx =[(1/(2n))tan^(2n) x]_0 ^(π/4) =(1/(2n)) ⇒u_n =(1/(2n))−u_(n−1) ⇒ u_n +u_(n−1 ) =(1/(2n)) ⇒Σ_(k=1) ^n (−1)^k (u_k +u_(k−1) ) =(1/2)Σ_(k=1) ^n (((−1)^k )/k) ⇒ −(u_1 +u_0 )+(u_2 +u_1 )+...(−1)^(n−1) (u_(n−1) +u_(n−2) )+(−1)^n (u_n +u_(n−1) ) =(1/2)Σ_(k=1) ^n (((−1)^k )/k) ⇒−u_0 +(−1)^n u_n =(1/2)Σ_(k=1) ^n (((−1)^k )/k) ⇒ (−1)^n u_n =u_0 +(1/2)Σ_(k=1) ^n (((−1)^k )/k) u_0 =∫_0 ^(π/4) ((sinx)/(cosx))dx =[−ln∣cosx∣]_0 ^(π/4) =−ln((1/( (√2)))) =(1/2)ln(2) ⇒ (−1)^n u_n =(1/2)ln(2)+(1/2)Σ_(k=1) ^n (((−1)^k )/k) ⇒ u_n =∫_0 ^(π/4) tan^(2n+1) x dx =(−1)^n {((ln2)/2) +(1/2)Σ_(k=1) ^n (((−1)^k )/k)} n=4 ⇒∫_0 ^(π/4) tan^9 xdx=((ln2)/2) +(1/2)Σ_(k=1) ^4 (((−1)^k )/k) =((ln2)/2) +(1/2){−1+(1/2)−(1/3) +(1/4)} =((ln2)/2) +(1/2){−(4/3) +(3/4)} =((ln2)/2) +(1/2)(((−7)/(12))) =((ln2)/2)−(7/(24))
$$\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{tan}^{\mathrm{2n}+\mathrm{1}} \mathrm{xdx}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{tan}^{\mathrm{2n}−\mathrm{1}} \mathrm{x}\left(\mathrm{1}+\:\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{tan}^{\mathrm{2n}−\mathrm{1}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}−\mathrm{u}_{\mathrm{n}−\mathrm{1}} \:\:\mathrm{we}\:\mathrm{hsve} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2n}−\mathrm{1}} \mathrm{dx}\:=\left[\frac{\mathrm{1}}{\mathrm{2n}}\mathrm{tan}^{\mathrm{2n}} \mathrm{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\frac{\mathrm{1}}{\mathrm{2n}}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2n}}−\mathrm{u}_{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} +\mathrm{u}_{\mathrm{n}−\mathrm{1}\:} =\frac{\mathrm{1}}{\mathrm{2n}}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(−\mathrm{1}\right)^{\mathrm{k}} \left(\mathrm{u}_{\mathrm{k}} +\mathrm{u}_{\mathrm{k}−\mathrm{1}} \right)\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\:\Rightarrow \\ $$$$−\left(\mathrm{u}_{\mathrm{1}} +\mathrm{u}_{\mathrm{0}} \right)+\left(\mathrm{u}_{\mathrm{2}} +\mathrm{u}_{\mathrm{1}} \right)+…\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\mathrm{u}_{\mathrm{n}−\mathrm{1}} +\mathrm{u}_{\mathrm{n}−\mathrm{2}} \right)+\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{u}_{\mathrm{n}} +\mathrm{u}_{\mathrm{n}−\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\:\Rightarrow−\mathrm{u}_{\mathrm{0}} \:+\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\:\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}_{\mathrm{n}} =\mathrm{u}_{\mathrm{0}} +\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}} \\ $$$$\mathrm{u}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{sinx}}{\mathrm{cosx}}\mathrm{dx}\:=\left[−\mathrm{ln}\mid\mathrm{cosx}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=−\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{tan}^{\mathrm{2n}+\mathrm{1}} \mathrm{x}\:\mathrm{dx}\:=\left(−\mathrm{1}\right)^{\mathrm{n}} \left\{\frac{\mathrm{ln2}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\right\} \\ $$$$\mathrm{n}=\mathrm{4}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{tan}^{\mathrm{9}} \mathrm{xdx}=\frac{\mathrm{ln2}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{4}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}} \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\right\}\:=\frac{\mathrm{ln2}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\mathrm{4}}{\mathrm{3}}\:+\frac{\mathrm{3}}{\mathrm{4}}\right\} \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{−\mathrm{7}}{\mathrm{12}}\right)\:=\frac{\mathrm{ln2}}{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{24}} \\ $$
Answered by Dwaipayan Shikari last updated on 01/Oct/20
∫_0 ^(π/4) ((sin^9 x)/(cos^9 x))dx=−∫_0 ^(π/4) ((sin^8 x(−sinx))/(cos^9 x))dx −∫_1 ^(1/( (√2))) (((1−t^2 )^4 )/t^9 )dt=∫_(1/( (√2))) ^1 (1/t^9 )−(4/t^7 )+(6/t^5 )−(4/t^3 )+(1/t) =[−(1/(8t^(8 ) ))+(2/(3t^6 ))−(3/(2t^4 ))+(2/t^2 )+log(t)]_(1/( (√2))) ^1 =log((√2))−(7/(24))
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{sin}^{\mathrm{9}} \mathrm{x}}{\mathrm{cos}^{\mathrm{9}} \mathrm{x}}\mathrm{dx}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{sin}^{\mathrm{8}} \mathrm{x}\left(−\mathrm{sinx}\right)}{\mathrm{cos}^{\mathrm{9}} \mathrm{x}}\mathrm{dx} \\ $$$$−\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{4}} }{\mathrm{t}^{\mathrm{9}} }\mathrm{dt}=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{t}^{\mathrm{9}} }−\frac{\mathrm{4}}{\mathrm{t}^{\mathrm{7}} }+\frac{\mathrm{6}}{\mathrm{t}^{\mathrm{5}} }−\frac{\mathrm{4}}{\mathrm{t}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{t}} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{8t}^{\mathrm{8}\:} }+\frac{\mathrm{2}}{\mathrm{3t}^{\mathrm{6}} }−\frac{\mathrm{3}}{\mathrm{2t}^{\mathrm{4}} }+\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} }+\mathrm{log}\left(\mathrm{t}\right)\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} =\mathrm{log}\left(\sqrt{\mathrm{2}}\right)−\frac{\mathrm{7}}{\mathrm{24}} \\ $$$$ \\ $$$$ \\ $$
Answered by maths mind last updated on 01/Oct/20
∫_0 ^(π/4) tg^a (x)dx=f(a),a∈C Re(a)≥0 tg(x)=t⇒f(a)=∫_0 ^1 (t^a /(1+t^2 ))dt=∫_0 ^1 Σ_(m≥0) (−t^2 )^m t^a dt =Σ_(m≥0) (−1)^m ∫_0 ^1 t^(2m+a) dt =Σ_(m≥0) (((−1)^m )/(2m+a+1))=Σ_(m≥0) ((1/(4m+a+1))−(1/(4m+a+3))) =(1/4)Σ_(m≥0) (((((a+3)/4)−((a+1)/4))/((m+((a+1)/4))(m+((a+2)/4)))))=(2/(16)).((Ψ(((a+3)/4))−Ψ(((a+1)/4)))/(((a+3)/4)−((a+1)/4))) =((Ψ(((a+3)/4))−𝚿(((a+1)/4)))/4)=f(a) f(9)=((Ψ(((12)/4))−Ψ(((10)/4)))/4) Ψ(z+1)=Ψ(z)+(1/z) Ψ(3)=−γ+1+(1/2)=(3/2)−γ Ψ(((10)/4))=Ψ((5/2))=Ψ((3/2))+(2/3)=(2/3)+2+Ψ((1/2)),Ψ((1/2))=−2ln(2)−γ Ψ(3)−Ψ((5/2))=(3/2)−γ−(2/3)−2−Ψ((1/2))=(3/2)−γ−(8/3)+2ln(2)+γ =((−7)/6)+2ln(2) f(9)=((−7+12ln(2))/(24))=−(7/(24))+((ln(2))/2)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}^{{a}} \left({x}\right){dx}={f}\left({a}\right),{a}\in\mathbb{C}\:\:{Re}\left({a}\right)\geqslant\mathrm{0} \\ $$$${tg}\left({x}\right)={t}\Rightarrow{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{a}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{m}\geqslant\mathrm{0}} {\sum}\left(−{t}^{\mathrm{2}} \right)^{{m}} {t}^{{a}} {dt} \\ $$$$=\underset{{m}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{m}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{m}+{a}} {dt} \\ $$$$=\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{m}} }{\mathrm{2}{m}+{a}+\mathrm{1}}=\underset{{m}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{4}{m}+{a}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}{m}+{a}+\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{{m}\geqslant\mathrm{0}} {\sum}\left(\frac{\frac{{a}+\mathrm{3}}{\mathrm{4}}−\frac{{a}+\mathrm{1}}{\mathrm{4}}}{\left({m}+\frac{{a}+\mathrm{1}}{\mathrm{4}}\right)\left({m}+\frac{{a}+\mathrm{2}}{\mathrm{4}}\right)}\right)=\frac{\mathrm{2}}{\mathrm{16}}.\frac{\Psi\left(\frac{{a}+\mathrm{3}}{\mathrm{4}}\right)−\Psi\left(\frac{{a}+\mathrm{1}}{\mathrm{4}}\right)}{\frac{{a}+\mathrm{3}}{\mathrm{4}}−\frac{{a}+\mathrm{1}}{\mathrm{4}}} \\ $$$$=\frac{\Psi\left(\frac{{a}+\mathrm{3}}{\mathrm{4}}\right)−\boldsymbol{\Psi}\left(\frac{{a}+\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}}={f}\left({a}\right) \\ $$$${f}\left(\mathrm{9}\right)=\frac{\Psi\left(\frac{\mathrm{12}}{\mathrm{4}}\right)−\Psi\left(\frac{\mathrm{10}}{\mathrm{4}}\right)}{\mathrm{4}} \\ $$$$\Psi\left({z}+\mathrm{1}\right)=\Psi\left({z}\right)+\frac{\mathrm{1}}{{z}} \\ $$$$\Psi\left(\mathrm{3}\right)=−\gamma+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}−\gamma \\ $$$$\Psi\left(\frac{\mathrm{10}}{\mathrm{4}}\right)=\Psi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\Psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}+\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right),\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{2}{ln}\left(\mathrm{2}\right)−\gamma \\ $$$$\Psi\left(\mathrm{3}\right)−\Psi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{2}}−\gamma−\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{2}}−\gamma−\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{2}{ln}\left(\mathrm{2}\right)+\gamma \\ $$$$=\frac{−\mathrm{7}}{\mathrm{6}}+\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$${f}\left(\mathrm{9}\right)=\frac{−\mathrm{7}+\mathrm{12}{ln}\left(\mathrm{2}\right)}{\mathrm{24}}=−\frac{\mathrm{7}}{\mathrm{24}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 02/Oct/20
very nice ..thank you so much....
$${very}\:{nice}\:..{thank}\:{you}\:{so} \\ $$$${much}…. \\ $$
Answered by 1549442205PVT last updated on 02/Oct/20
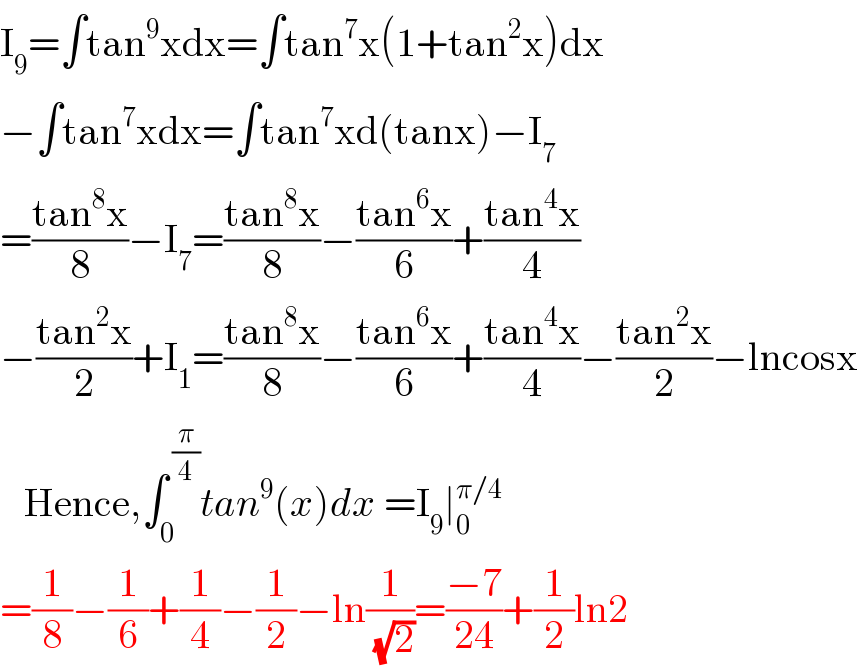
I_9 =∫tan^9 xdx=∫tan^7 x(1+tan^2 x)dx −∫tan^7 xdx=∫tan^7 xd(tanx)−I_7 =((tan^8 x)/8)−I_7 =((tan^8 x)/8)−((tan^6 x)/6)+((tan^4 x)/4) −((tan^2 x)/2)+I_1 =((tan^8 x)/8)−((tan^6 x)/6)+((tan^4 x)/4)−((tan^2 x)/2)−lncosx Hence,∫_0 ^( (π/4)) tan^9 (x)dx =I_9 ∣_0 ^(π/4) =(1/8)−(1/6)+(1/4)−(1/2)−ln(1/( (√2)))=((−7)/(24))+(1/2)ln2
$$\mathrm{I}_{\mathrm{9}} =\int\mathrm{tan}^{\mathrm{9}} \mathrm{xdx}=\int\mathrm{tan}^{\mathrm{7}} \mathrm{x}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\: \\ $$$$−\int\mathrm{tan}^{\mathrm{7}} \mathrm{xdx}=\int\mathrm{tan}^{\mathrm{7}} \mathrm{xd}\left(\mathrm{tanx}\right)−\mathrm{I}_{\mathrm{7}} \\ $$$$=\frac{\mathrm{tan}^{\mathrm{8}} \mathrm{x}}{\mathrm{8}}−\mathrm{I}_{\mathrm{7}} =\frac{\mathrm{tan}^{\mathrm{8}} \mathrm{x}}{\mathrm{8}}−\frac{\mathrm{tan}^{\mathrm{6}} \mathrm{x}}{\mathrm{6}}+\frac{\mathrm{tan}^{\mathrm{4}} \mathrm{x}}{\mathrm{4}} \\ $$$$−\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}+\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{tan}^{\mathrm{8}} \mathrm{x}}{\mathrm{8}}−\frac{\mathrm{tan}^{\mathrm{6}} \mathrm{x}}{\mathrm{6}}+\frac{\mathrm{tan}^{\mathrm{4}} \mathrm{x}}{\mathrm{4}}−\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}−\mathrm{lncosx} \\ $$$$\:\:\:\mathrm{Hence},\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {tan}^{\mathrm{9}} \left({x}\right){dx}\:=\mathrm{I}_{\mathrm{9}} \mid_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{ln}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{−\mathrm{7}}{\mathrm{24}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln2} \\ $$
Commented by mnjuly1970 last updated on 02/Oct/20
thanks a lot
$${thanks}\:{a}\:{lot}\:\: \\ $$
Commented by 1549442205PVT last updated on 07/Oct/20
You are welcome.
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *