Question Number 20167 by tammi last updated on 23/Aug/17
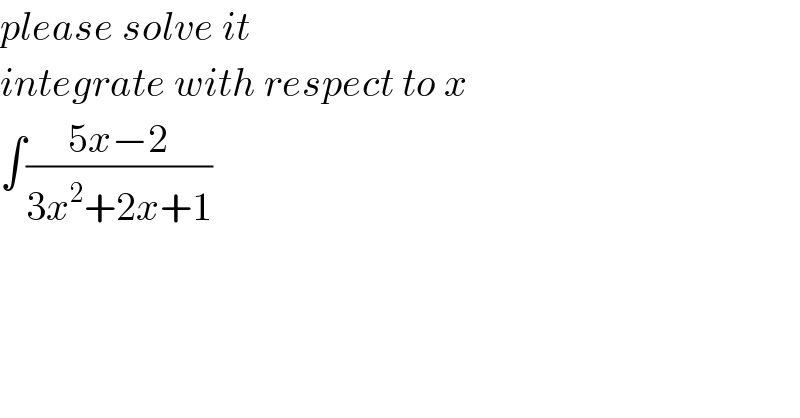
$${please}\:{solve}\:{it} \\ $$$${integrate}\:{with}\:{respect}\:{to}\:{x} \\ $$$$\int\frac{\mathrm{5}{x}−\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}} \\ $$
Answered by ajfour last updated on 23/Aug/17
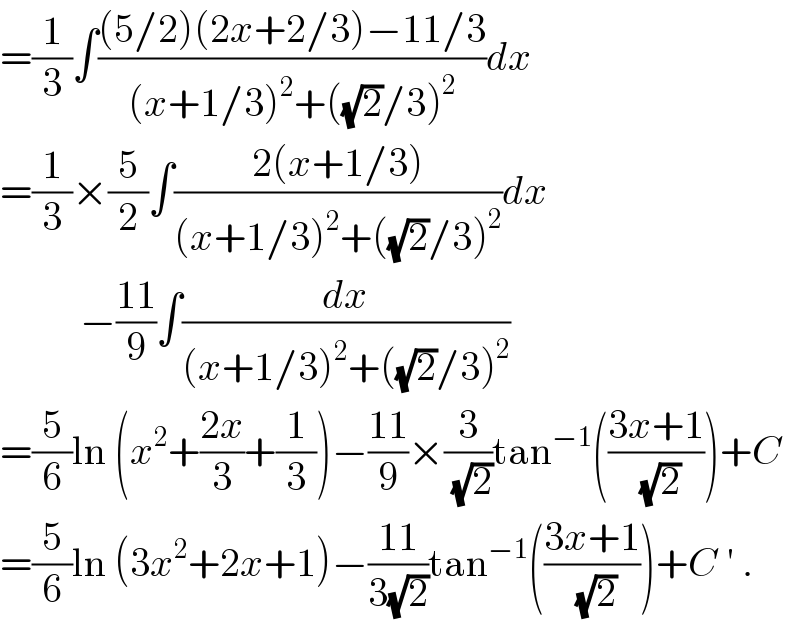
$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\left(\mathrm{5}/\mathrm{2}\right)\left(\mathrm{2}{x}+\mathrm{2}/\mathrm{3}\right)−\mathrm{11}/\mathrm{3}}{\left({x}+\mathrm{1}/\mathrm{3}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}/\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{5}}{\mathrm{2}}\int\frac{\mathrm{2}\left({x}+\mathrm{1}/\mathrm{3}\right)}{\left({x}+\mathrm{1}/\mathrm{3}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}/\mathrm{3}\right)^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{11}}{\mathrm{9}}\int\frac{{dx}}{\left({x}+\mathrm{1}/\mathrm{3}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}/\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\frac{\mathrm{2}{x}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\right)−\frac{\mathrm{11}}{\mathrm{9}}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}+\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)−\frac{\mathrm{11}}{\mathrm{3}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}+\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+{C}\:'\:. \\ $$
Commented by tammi last updated on 23/Aug/17

$${thanksss} \\ $$
