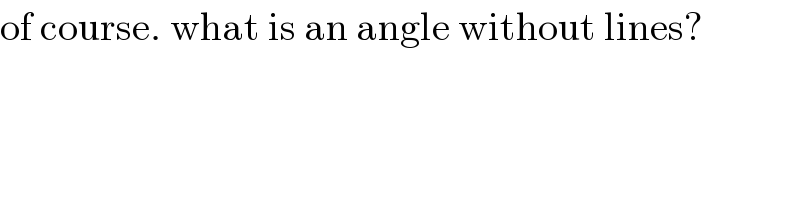please-what-is-the-fomula-to-determinate-the-equations-of-bissectors-in-triangle-

Question Number 78820 by mathocean1 last updated on 20/Jan/20

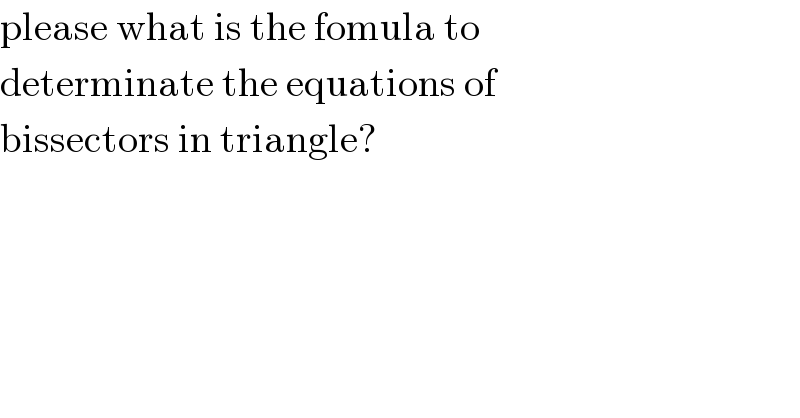
please what is the fomula to

determinate the equations of

bissectors in triangle ?

Answered by MJS last updated on 21/Jan/20

bisector between 2 lines

l_{1} : y = a_{1} x + c_{1}

l_{2} : y = a_{2} x + c_{2}

intersection :

I = (\begin{matrix} \frac{c_{2} - c_{1}}{a_{1} - a_{2}} \\ \frac{a_{1} c_{2} - a_{2} c_{1}}{a_{1} - a_{2}} \end{matrix})

direction vectors :

v_{1} = (\begin{matrix} 1 \\ a_{1} \end{matrix}); v_{2} = (\begin{matrix} 1 \\ a_{2} \end{matrix})

normalized :

v_{1} = (\begin{matrix} \frac{1}{\sqrt{1 + a_{1}^{2}}} \\ \frac{a_{1}}{\sqrt{1 + a_{1}^{2}}} \end{matrix}); v_{2} = (\begin{matrix} \frac{1}{\sqrt{1 + a_{2}^{2}}} \\ \frac{a_{1}}{\sqrt{1 + a_{2}^{2}}} \end{matrix})

direction vectors of bisectors

v_{b 1} = v_{1} + v_{2} = (\begin{matrix} p \\ q \end{matrix})

v_{b 2} = (\begin{matrix} q \\ - p \end{matrix})

bisectors

l_{b 1} : X = I + {t v}_{b 1}

l_{b 2} : X = I + {t v}_{b 2}

Commented by jagoll last updated on 21/Jan/20

good sir

Commented by mathocean1 last updated on 21/Jan/20

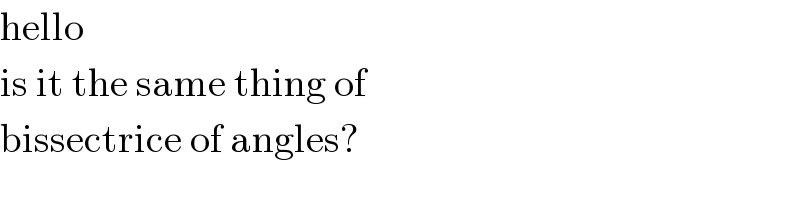
hello

is it the same thing of

bissectrice of angles ?

Commented by MJS last updated on 21/Jan/20

of course . what is an angle without lines ?

Facebook Tweet Pin