Question Number 184944 by SANOGO last updated on 14/Jan/23
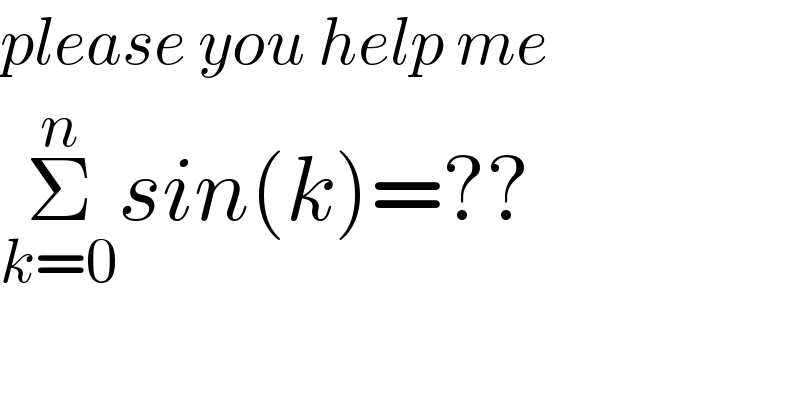
$${please}\:{you}\:{help}\:{me} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{sin}\left({k}\right)=?? \\ $$
Answered by JDamian last updated on 15/Jan/23
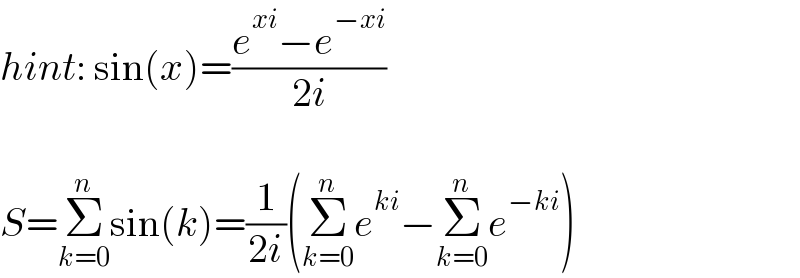
$${hint}:\:\mathrm{sin}\left({x}\right)=\frac{{e}^{{xi}} −{e}^{−{xi}} }{\mathrm{2}{i}} \\ $$$$ \\ $$$${S}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{sin}\left({k}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{ki}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{−{ki}} \right) \\ $$
