Question Number 64477 by Chi Mes Try last updated on 18/Jul/19

$${pls}\:\:{i}\:{need}\:{it}\:{urgently}…\:{am}\:{stuck} \\ $$$${workings}\:{please} \\ $$$$\left(\mathrm{1}\right)\:\:\int{Ln}\left(\mathrm{1}−{Lnx}\right){dx} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\:\int\frac{\mathrm{1}}{{Lnx}}{dx} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\int\:{Ln}\left(−\mathrm{2}{Lnx}\right){dx} \\ $$$$ \\ $$$${God}\:{will}\:{honour}\:{u}\:\mathrm{4}\:{ur}\:{replies} \\ $$
Commented by Prithwish sen last updated on 18/Jul/19
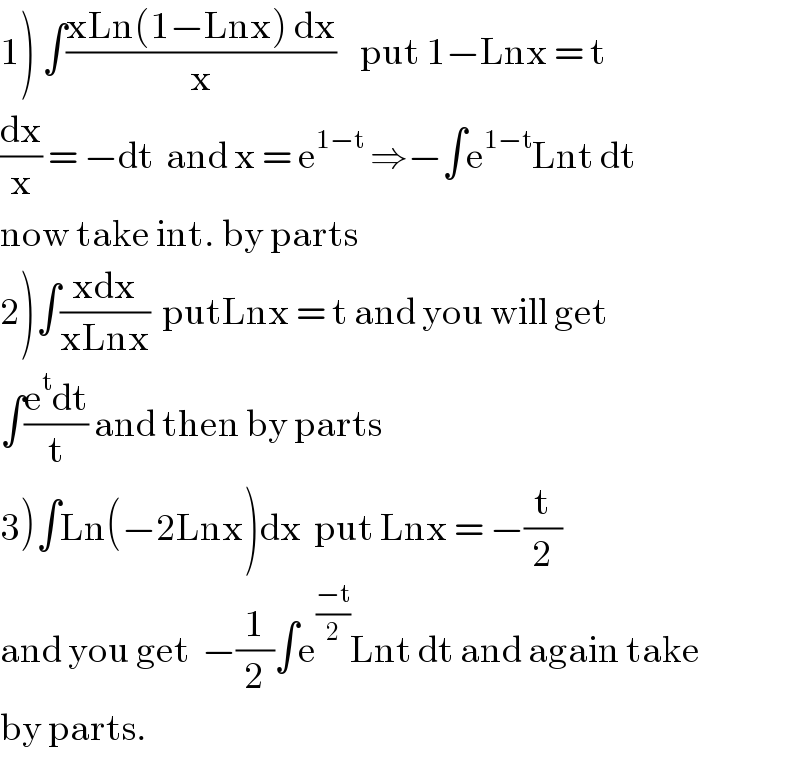
$$\left.\mathrm{1}\right)\:\int\frac{\mathrm{xLn}\left(\mathrm{1}−\mathrm{Lnx}\right)\:\mathrm{dx}}{\mathrm{x}}\:\:\:\:\mathrm{put}\:\mathrm{1}−\mathrm{Lnx}\:=\:\mathrm{t} \\ $$$$\frac{\mathrm{dx}}{\mathrm{x}}\:=\:−\mathrm{dt}\:\:\mathrm{and}\:\mathrm{x}\:=\:\mathrm{e}^{\mathrm{1}−\mathrm{t}} \:\Rightarrow−\int\mathrm{e}^{\mathrm{1}−\mathrm{t}} \mathrm{Lnt}\:\mathrm{dt} \\ $$$$\mathrm{now}\:\mathrm{take}\:\mathrm{int}.\:\mathrm{by}\:\mathrm{parts} \\ $$$$\left.\mathrm{2}\right)\int\frac{\mathrm{xdx}}{\mathrm{xLnx}}\:\:\mathrm{putLnx}\:=\:\mathrm{t}\:\mathrm{and}\:\mathrm{you}\:\mathrm{will}\:\mathrm{get} \\ $$$$\int\frac{\mathrm{e}^{\mathrm{t}} \mathrm{dt}}{\mathrm{t}}\:\mathrm{and}\:\mathrm{then}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\left.\mathrm{3}\right)\int\mathrm{Ln}\left(−\mathrm{2Lnx}\right)\mathrm{dx}\:\:\mathrm{put}\:\mathrm{Lnx}\:=\:−\frac{\mathrm{t}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{you}\:\mathrm{get}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{e}^{\frac{−\mathrm{t}}{\mathrm{2}}} \mathrm{Lnt}\:\mathrm{dt}\:\mathrm{and}\:\mathrm{again}\:\mathrm{take}\: \\ $$$$\mathrm{by}\:\mathrm{parts}. \\ $$
