Menu Close

posons-1-2-3-n-a-n-b-n-3-montre-que-pgcd-a-n-b-n-1-

Tinku Tara 0 Comments
Pin




Question Number 87878 by Cmr 237 last updated on 06/Apr/20
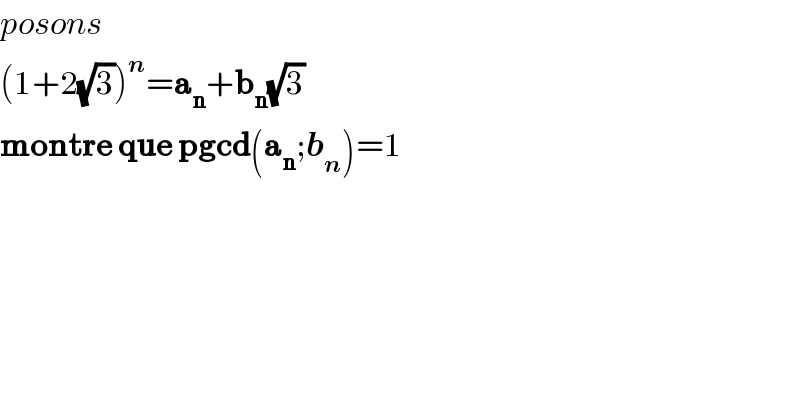
posons (1+2(√3))^n =a_n +b_n (√3) montre que pgcd(a_n ;b_n )=1
$${posons}\: \\ $$$$\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\right)^{\boldsymbol{{n}}} =\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} +\boldsymbol{\mathrm{b}}_{\boldsymbol{\mathrm{n}}} \sqrt{\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{montre}}\:\boldsymbol{\mathrm{que}}\:\boldsymbol{\mathrm{pgcd}}\left(\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} ;\boldsymbol{{b}}_{\boldsymbol{{n}}} \right)=\mathrm{1} \\ $$
Answered by mind is power last updated on 07/Apr/20
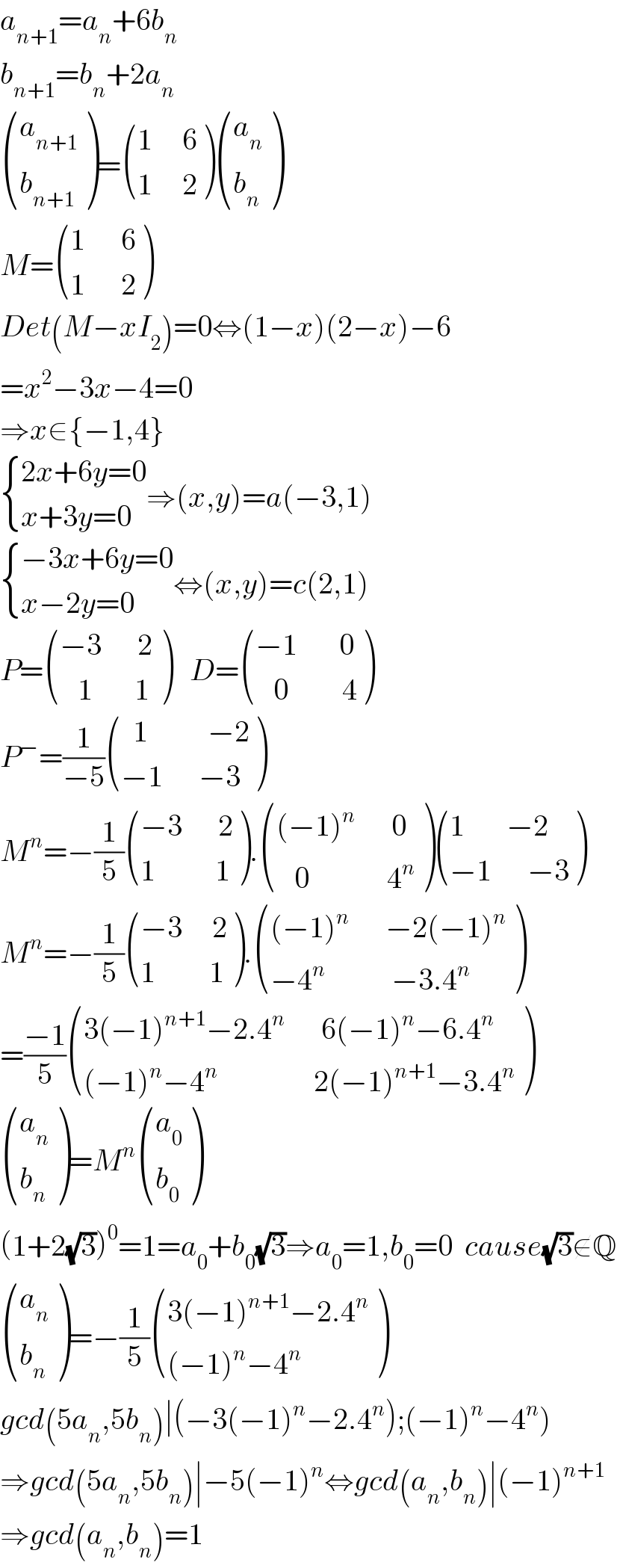
a_(n+1) =a_n +6b_n b_(n+1) =b_n +2a_n ((a_(n+1) ),(b_(n+1) ) )= (((1 6)),((1 2)) ) ((a_n ),(b_n ) ) M= (((1 6)),((1 2)) ) Det(M−xI_2 )=0⇔(1−x)(2−x)−6 =x^2 −3x−4=0 ⇒x∈{−1,4} { ((2x+6y=0)),((x+3y=0)) :}⇒(x,y)=a(−3,1) { ((−3x+6y=0)),((x−2y=0)) :}⇔(x,y)=c(2,1) P= (((−3 2)),(( 1 1 )) ) D= (((−1 0)),(( 0 4)) ) P^− =(1/(−5)) ((( 1 −2)),((−1 −3)) ) M^n =−(1/5) (((−3 2)),((1 1)) ). ((((−1)^n 0)),(( 0 4^n )) ) (((1 −2)),((−1 −3)) ) M^n =−(1/5) (((−3 2)),((1 1)) ). ((((−1)^n −2(−1)^n )),((−4^n −3.4^n )) ) =((−1)/5) (((3(−1)^(n+1) −2.4^n 6(−1)^n −6.4^n )),(((−1)^n −4^n 2(−1)^(n+1) −3.4^n )) ) ((a_n ),(b_n ) )=M^n ((a_0 ),(b_0 ) ) (1+2(√3))^0 =1=a_0 +b_0 (√3)⇒a_0 =1,b_0 =0 cause(√3)∉Q ((a_n ),(b_n ) )=−(1/5) (((3(−1)^(n+1) −2.4^n )),(((−1)^n −4^n )) ) gcd(5a_n ,5b_n )∣(−3(−1)^n −2.4^n );(−1)^n −4^n ) ⇒gcd(5a_n ,5b_n )∣−5(−1)^n ⇔gcd(a_n ,b_n )∣(−1)^(n+1) ⇒gcd(a_n ,b_n )=1
$${a}_{{n}+\mathrm{1}} ={a}_{{n}} +\mathrm{6}{b}_{{n}} \\ $$$${b}_{{n}+\mathrm{1}} ={b}_{{n}} +\mathrm{2}{a}_{{n}} \\ $$$$\begin{pmatrix}{{a}_{{n}+\mathrm{1}} }\\{{b}_{{n}+\mathrm{1}} }\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{6}}\\{\mathrm{1}\:\:\:\:\:\mathrm{2}}\end{pmatrix}\begin{pmatrix}{{a}_{{n}} }\\{{b}_{{n}} }\end{pmatrix} \\ $$$${M}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\mathrm{6}}\\{\mathrm{1}\:\:\:\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$${Det}\left({M}−{xI}_{\mathrm{2}} \right)=\mathrm{0}\Leftrightarrow\left(\mathrm{1}−{x}\right)\left(\mathrm{2}−{x}\right)−\mathrm{6} \\ $$$$={x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{x}\in\left\{−\mathrm{1},\mathrm{4}\right\} \\ $$$$\begin{cases}{\mathrm{2}{x}+\mathrm{6}{y}=\mathrm{0}}\\{{x}+\mathrm{3}{y}=\mathrm{0}}\end{cases}\Rightarrow\left({x},{y}\right)={a}\left(−\mathrm{3},\mathrm{1}\right) \\ $$$$\begin{cases}{−\mathrm{3}{x}+\mathrm{6}{y}=\mathrm{0}}\\{{x}−\mathrm{2}{y}=\mathrm{0}}\end{cases}\Leftrightarrow\left({x},{y}\right)={c}\left(\mathrm{2},\mathrm{1}\right) \\ $$$${P}=\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{2}}\\{\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:}\end{pmatrix}\:\:\:{D}=\begin{pmatrix}{−\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{4}}\end{pmatrix} \\ $$$${P}^{−} =\frac{\mathrm{1}}{−\mathrm{5}}\begin{pmatrix}{\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:−\mathrm{2}}\\{−\mathrm{1}\:\:\:\:\:\:−\mathrm{3}}\end{pmatrix}\: \\ $$$${M}^{{n}} =−\frac{\mathrm{1}}{\mathrm{5}}\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}.\begin{pmatrix}{\left(−\mathrm{1}\right)^{{n}} \:\:\:\:\:\:\mathrm{0}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}^{{n}} }\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:−\mathrm{2}}\\{−\mathrm{1}\:\:\:\:\:\:−\mathrm{3}}\end{pmatrix} \\ $$$${M}^{{n}} =−\frac{\mathrm{1}}{\mathrm{5}}\begin{pmatrix}{−\mathrm{3}\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}.\begin{pmatrix}{\left(−\mathrm{1}\right)^{{n}} \:\:\:\:\:\:−\mathrm{2}\left(−\mathrm{1}\right)^{{n}} }\\{−\mathrm{4}^{{n}} \:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}.\mathrm{4}^{{n}} }\end{pmatrix} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{5}}\begin{pmatrix}{\mathrm{3}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\mathrm{2}.\mathrm{4}^{{n}} \:\:\:\:\:\:\mathrm{6}\left(−\mathrm{1}\right)^{{n}} −\mathrm{6}.\mathrm{4}^{{n}} }\\{\left(−\mathrm{1}\right)^{{n}} −\mathrm{4}^{{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\mathrm{3}.\mathrm{4}^{{n}} }\end{pmatrix} \\ $$$$\begin{pmatrix}{{a}_{{n}} }\\{{b}_{{n}} }\end{pmatrix}={M}^{{n}} \begin{pmatrix}{{a}_{\mathrm{0}} }\\{{b}_{\mathrm{0}} }\end{pmatrix} \\ $$$$\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{0}} =\mathrm{1}={a}_{\mathrm{0}} +{b}_{\mathrm{0}} \sqrt{\mathrm{3}}\Rightarrow{a}_{\mathrm{0}} =\mathrm{1},{b}_{\mathrm{0}} =\mathrm{0}\:\:{cause}\sqrt{\mathrm{3}}\notin\mathbb{Q} \\ $$$$\begin{pmatrix}{{a}_{{n}} }\\{{b}_{{n}} }\end{pmatrix}=−\frac{\mathrm{1}}{\mathrm{5}}\begin{pmatrix}{\mathrm{3}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\mathrm{2}.\mathrm{4}^{{n}} }\\{\left(−\mathrm{1}\right)^{{n}} −\mathrm{4}^{{n}} }\end{pmatrix} \\ $$$$\left.{gcd}\left(\mathrm{5}{a}_{{n}} ,\mathrm{5}{b}_{{n}} \right)\mid\left(−\mathrm{3}\left(−\mathrm{1}\right)^{{n}} −\mathrm{2}.\mathrm{4}^{{n}} \right);\left(−\mathrm{1}\right)^{{n}} −\mathrm{4}^{{n}} \right) \\ $$$$\Rightarrow{gcd}\left(\mathrm{5}{a}_{{n}} ,\mathrm{5}{b}_{{n}} \right)\mid−\mathrm{5}\left(−\mathrm{1}\right)^{{n}} \Leftrightarrow{gcd}\left({a}_{{n}} ,{b}_{{n}} \right)\mid\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$$$\Rightarrow{gcd}\left({a}_{{n}} ,{b}_{{n}} \right)=\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *