Product-of-n-n-th-roots-of-unity-1-2-3-n-1-1-n-1-Why-How-to-get-RHS-

Question Number 19312 by Tinkutara last updated on 09/Aug/17

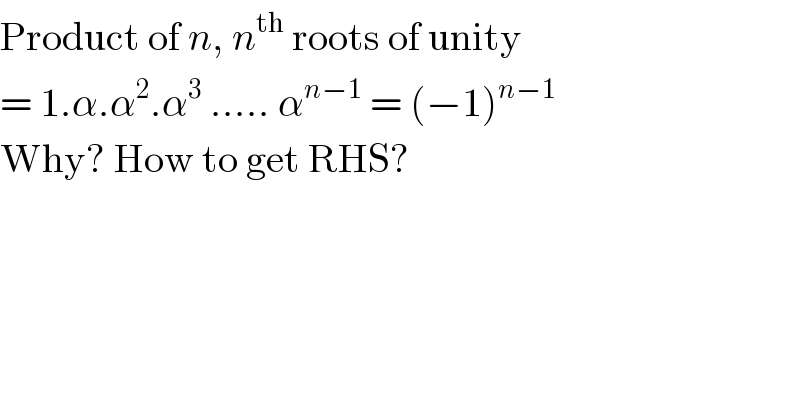
Product of n, n^(th) roots of unity = 1.α.α^2 .α^3 ..... α^(n−1) = (−1)^(n−1) Why? How to get RHS?

$$\mathrm{Product}\:\mathrm{of}\:{n},\:{n}^{\mathrm{th}} \:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity} \\ $$$$=\:\mathrm{1}.\alpha.\alpha^{\mathrm{2}} .\alpha^{\mathrm{3}} \:…..\:\alpha^{{n}−\mathrm{1}} \:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \\ $$$$\mathrm{Why}?\:\mathrm{How}\:\mathrm{to}\:\mathrm{get}\:\mathrm{RHS}? \\ $$

Answered by ajfour last updated on 09/Aug/17

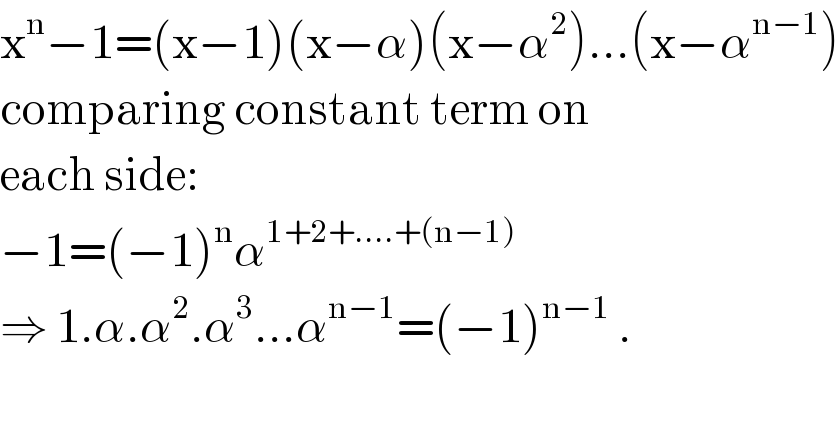
x^n −1=(x−1)(x−α)(x−α^2 )...(x−α^(n−1) ) comparing constant term on each side: −1=(−1)^n α^(1+2+....+(n−1)) ⇒ 1.α.α^2 .α^3 ...α^(n−1) =(−1)^(n−1) .

$$\mathrm{x}^{\mathrm{n}} −\mathrm{1}=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\alpha\right)\left(\mathrm{x}−\alpha^{\mathrm{2}} \right)…\left(\mathrm{x}−\alpha^{\mathrm{n}−\mathrm{1}} \right) \\ $$$$\mathrm{comparing}\:\mathrm{constant}\:\mathrm{term}\:\mathrm{on} \\ $$$$\mathrm{each}\:\mathrm{side}: \\ $$$$−\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{n}} \alpha^{\mathrm{1}+\mathrm{2}+….+\left(\mathrm{n}−\mathrm{1}\right)} \\ $$$$\Rightarrow\:\mathrm{1}.\alpha.\alpha^{\mathrm{2}} .\alpha^{\mathrm{3}} …\alpha^{\mathrm{n}−\mathrm{1}} =\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 09/Aug/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Facebook Tweet Pin

Product-of-n-n-th-roots-of-unity-1-2-3-n-1-1-n-1-Why-How-to-get-RHS-

Leave a Reply Cancel reply