Question Number 27271 by GANGADHARSETHI last updated on 04/Jan/18
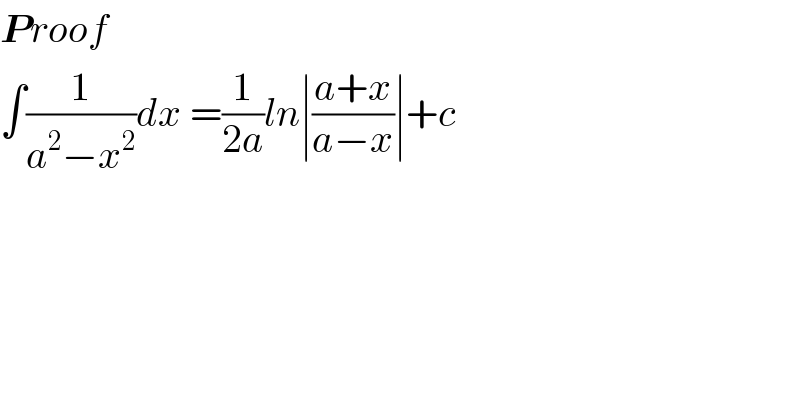
$$\boldsymbol{{P}}{roof}\: \\ $$$$\int\frac{\mathrm{1}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}\:=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\mid\frac{{a}+{x}}{{a}−{x}}\mid+{c} \\ $$
Answered by sma3l2996 last updated on 04/Jan/18
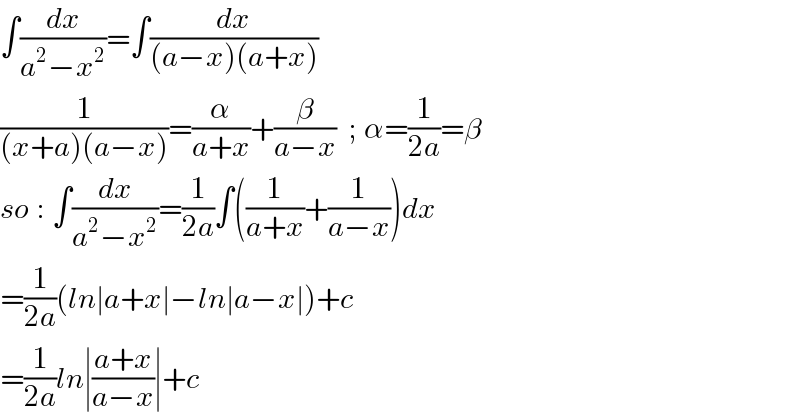
$$\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\int\frac{{dx}}{\left({a}−{x}\right)\left({a}+{x}\right)} \\ $$$$\frac{\mathrm{1}}{\left({x}+{a}\right)\left({a}−{x}\right)}=\frac{\alpha}{{a}+{x}}+\frac{\beta}{{a}−{x}}\:\:;\:\alpha=\frac{\mathrm{1}}{\mathrm{2}{a}}=\beta \\ $$$${so}\::\:\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{a}}\int\left(\frac{\mathrm{1}}{{a}+{x}}+\frac{\mathrm{1}}{{a}−{x}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}\left({ln}\mid{a}+{x}\mid−{ln}\mid{a}−{x}\mid\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\mid\frac{{a}+{x}}{{a}−{x}}\mid+{c} \\ $$
