Question Number 111954 by Hassen_Timol last updated on 05/Sep/20
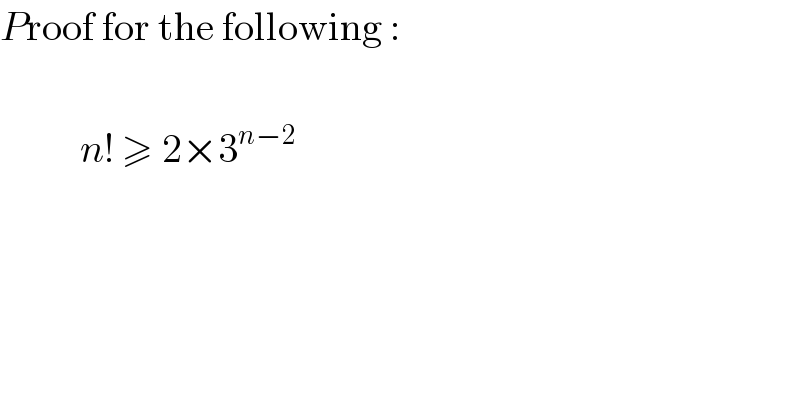
$${P}\mathrm{roof}\:\mathrm{for}\:\mathrm{the}\:\mathrm{following}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:{n}!\:\geqslant\:\mathrm{2}×\mathrm{3}^{{n}−\mathrm{2}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 05/Sep/20

$$\mathrm{by}\:\mathrm{recurence}\:\:\mathrm{n}=\mathrm{2}\:\:\:\mathrm{2}!\geqslant\mathrm{2}×\mathrm{1}\:\left(\mathrm{true}\right)\:\mathrm{let}\:\mathrm{suppose}\:\mathrm{n}!\geqslant\mathrm{2}.\mathrm{3}^{\mathrm{n}−\mathrm{2}} \\ $$$$\left(\mathrm{n}+\mathrm{1}\right)!\:=\left(\mathrm{n}+\mathrm{1}\right)\mathrm{n}!\:\geqslant\left(\mathrm{n}+\mathrm{1}\right)\mathrm{2}.\mathrm{3}^{\mathrm{n}−\mathrm{2}} \:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{3}^{\mathrm{n}−\mathrm{2}} −\mathrm{2}\:.\mathrm{3}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} \:=\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{3}^{\mathrm{n}−\mathrm{2}} −\mathrm{2}.\mathrm{3}^{\mathrm{n}−\mathrm{2}+\mathrm{1}} \\ $$$$=\mathrm{2}.\mathrm{3}^{\mathrm{n}−\mathrm{2}} \left\{\mathrm{n}+\mathrm{1}−\mathrm{3}\right\}\:=\mathrm{2}.\mathrm{3}^{\mathrm{n}−\mathrm{2}} \left(\mathrm{n}−\mathrm{2}\right)\:\geqslant\mathrm{0}\:\mathrm{due}\:\mathrm{to}\:\mathrm{n}\geqslant\mathrm{2}\:\Rightarrow \\ $$$$\left(\mathrm{n}+\mathrm{1}\right)!\geqslant\mathrm{2}.\mathrm{3}^{\mathrm{n}+\mathrm{1}−\mathrm{2}} \:\:\:\mathrm{the}\:\mathrm{relation}\:\mathrm{is}\:\mathrm{true}\:\:\mathrm{at}\:\mathrm{term}\:\left(\mathrm{n}+\mathrm{1}\right) \\ $$
Commented by aleks041103 last updated on 05/Sep/20

$${He}\:{used}\:{proof}\:{by}\:{induction} \\ $$
Commented by Hassen_Timol last updated on 05/Sep/20
Sorry but I don't understand I think... ��
Commented by mathmax by abdo last updated on 05/Sep/20

$$\:\mathrm{I}\:\mathrm{have}\:\mathrm{used}\:\mathrm{recurrence}\:\mathrm{method}… \\ $$
