Question Number 116891 by bemath last updated on 07/Oct/20
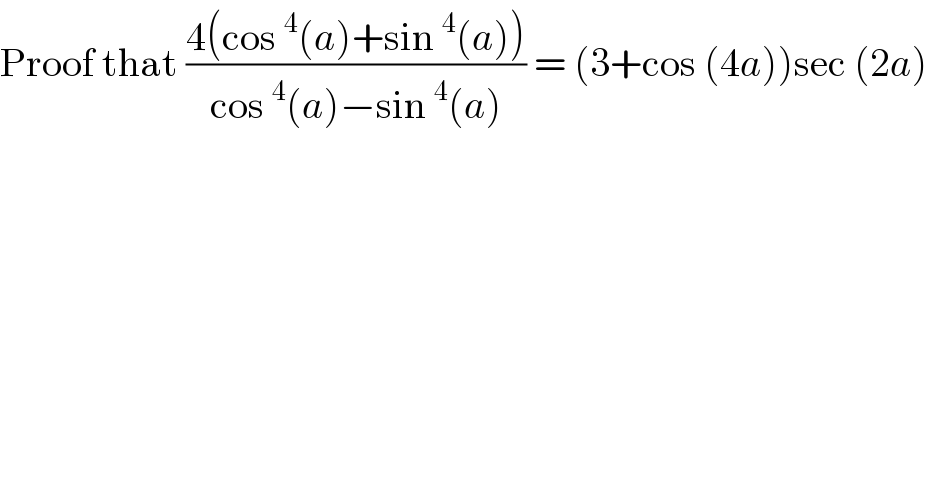
$$\mathrm{Proof}\:\mathrm{that}\:\frac{\mathrm{4}\left(\mathrm{cos}\:^{\mathrm{4}} \left({a}\right)+\mathrm{sin}\:^{\mathrm{4}} \left({a}\right)\right)}{\mathrm{cos}\:^{\mathrm{4}} \left({a}\right)−\mathrm{sin}\:^{\mathrm{4}} \left({a}\right)}\:=\:\left(\mathrm{3}+\mathrm{cos}\:\left(\mathrm{4}{a}\right)\right)\mathrm{sec}\:\left(\mathrm{2}{a}\right)\: \\ $$
Answered by john santu last updated on 07/Oct/20
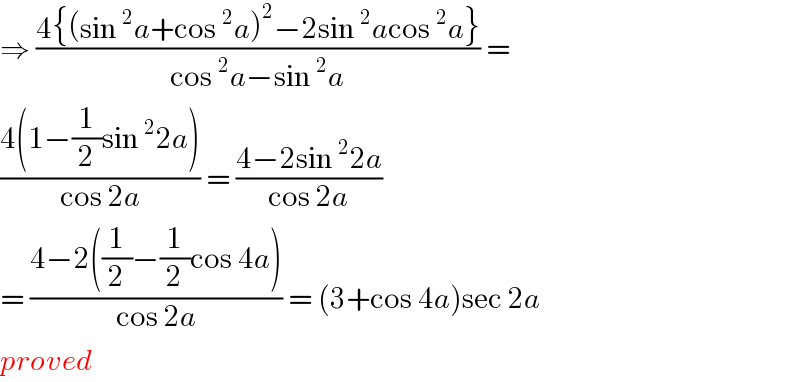
$$\Rightarrow\:\frac{\mathrm{4}\left\{\left(\mathrm{sin}\:^{\mathrm{2}} {a}+\mathrm{cos}\:^{\mathrm{2}} {a}\right)^{\mathrm{2}} −\mathrm{2sin}\:^{\mathrm{2}} {a}\mathrm{cos}\:^{\mathrm{2}} {a}\right\}}{\mathrm{cos}\:^{\mathrm{2}} {a}−\mathrm{sin}\:^{\mathrm{2}} {a}}\:= \\ $$$$\frac{\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{a}\right)}{\mathrm{cos}\:\mathrm{2}{a}}\:=\:\frac{\mathrm{4}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{a}}{\mathrm{cos}\:\mathrm{2}{a}} \\ $$$$=\:\frac{\mathrm{4}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4}{a}\right)}{\mathrm{cos}\:\mathrm{2}{a}}\:=\:\left(\mathrm{3}+\mathrm{cos}\:\mathrm{4}{a}\right)\mathrm{sec}\:\mathrm{2}{a} \\ $$$${proved} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Oct/20
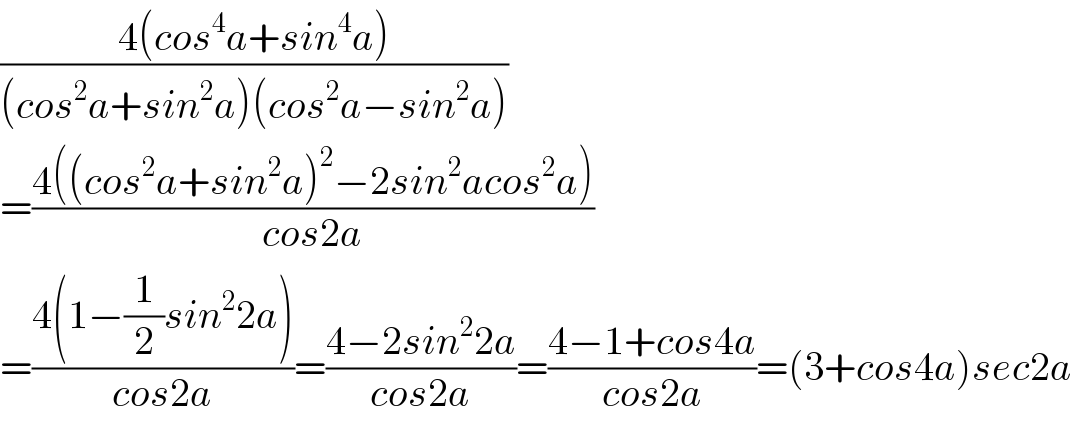
$$\frac{\mathrm{4}\left({cos}^{\mathrm{4}} {a}+{sin}^{\mathrm{4}} {a}\right)}{\left({cos}^{\mathrm{2}} {a}+{sin}^{\mathrm{2}} {a}\right)\left({cos}^{\mathrm{2}} {a}−{sin}^{\mathrm{2}} {a}\right)} \\ $$$$=\frac{\mathrm{4}\left(\left({cos}^{\mathrm{2}} {a}+{sin}^{\mathrm{2}} {a}\right)^{\mathrm{2}} −\mathrm{2}{sin}^{\mathrm{2}} {acos}^{\mathrm{2}} {a}\right)}{{cos}\mathrm{2}{a}} \\ $$$$=\frac{\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \mathrm{2}{a}\right)}{{cos}\mathrm{2}{a}}=\frac{\mathrm{4}−\mathrm{2}{sin}^{\mathrm{2}} \mathrm{2}{a}}{{cos}\mathrm{2}{a}}=\frac{\mathrm{4}−\mathrm{1}+{cos}\mathrm{4}{a}}{{cos}\mathrm{2}{a}}=\left(\mathrm{3}+{cos}\mathrm{4}{a}\right){sec}\mathrm{2}{a} \\ $$
