Question Number 19857 by Nayon last updated on 16/Aug/17
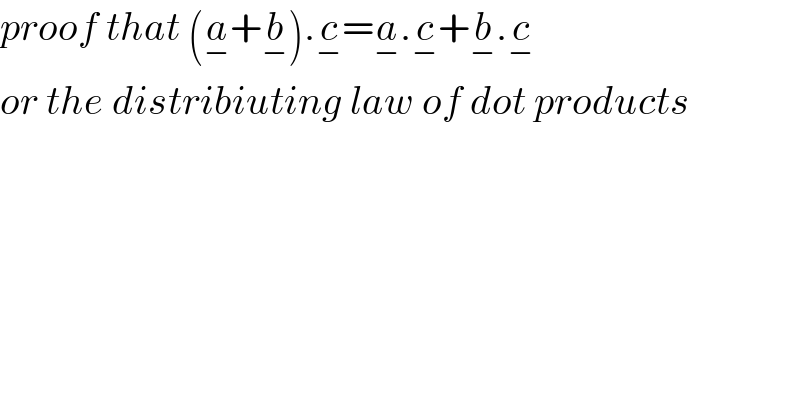
$${proof}\:{that}\:\left(\underset{−} {{a}}+\underset{−} {{b}}\right).\underset{−} {{c}}=\underset{−} {{a}}.\underset{−} {{c}}+\underset{−} {{b}}.\underset{−} {{c}} \\ $$$${or}\:{the}\:{distribiuting}\:{law}\:{of}\:{dot}\:{products} \\ $$$$ \\ $$
Commented by Nayon last updated on 16/Aug/17
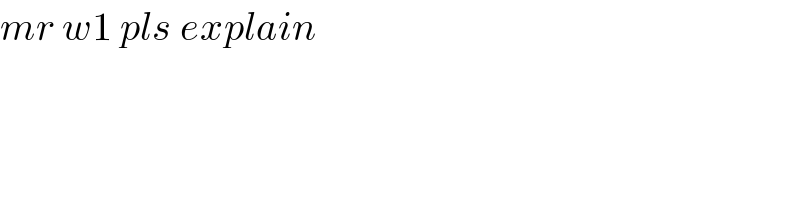
$${mr}\:{w}\mathrm{1}\:{pls}\:{explain} \\ $$
Commented by mrW1 last updated on 16/Aug/17

$$\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\right)\centerdot\boldsymbol{\mathrm{c}}=\mid\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{b}}\mid×\mathrm{cos}\:\theta×\mid\boldsymbol{\mathrm{c}}\mid \\ $$$$=\mathrm{PQ}×\mid\boldsymbol{\mathrm{c}}\mid \\ $$$$=\left(\mathrm{PQ}+\mathrm{QR}\right)×\mid\boldsymbol{\mathrm{c}}\mid \\ $$$$=\left(\mid\boldsymbol{\mathrm{a}}\mid×\mathrm{cos}\:\theta_{\mathrm{1}} +\mid\boldsymbol{\mathrm{b}}\mid×\mathrm{cos}\:\theta_{\mathrm{2}} \right)×\mid\boldsymbol{\mathrm{c}}\mid \\ $$$$=\mid\boldsymbol{\mathrm{a}}\mid×\mathrm{cos}\:\theta_{\mathrm{1}} ×\mid\boldsymbol{\mathrm{c}}\mid+\mid\boldsymbol{\mathrm{b}}\mid×\mathrm{cos}\:\theta_{\mathrm{2}} ×\mid\boldsymbol{\mathrm{c}}\mid \\ $$$$=\boldsymbol{\mathrm{a}}\centerdot\boldsymbol{\mathrm{c}}+\boldsymbol{\mathrm{b}}\centerdot\boldsymbol{\mathrm{c}} \\ $$
Commented by mrW1 last updated on 16/Aug/17

