Menu Close

proof-that-n-1-10-n-n-11-1-

Tinku Tara 0 Comments
Pin




Question Number 155803 by cortano last updated on 05/Oct/21
proof that Σ_(n=1) ^(10) n×n! = 11!−1
$$\mathrm{proof}\:\mathrm{that}\: \\ $$$$\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\mathrm{n}×\mathrm{n}!\:=\:\mathrm{11}!−\mathrm{1} \\ $$
Answered by som(math1967) last updated on 05/Oct/21
1×1!+2×2!+3×3!+...+10×10! +1−1 =2+2×2!+3×3!+...+10×10!−1 =2!(1+2)+3×3!+4×4!+...+10×10!−1 =3!+3×3!+4×4!+...+10×10!−1 =3!(1+3)+4×4!+...+10×10!−1 =4!(1+4)+5×5!+...+10×10!−1 =5!(1+5)+...+10×10!−1 =... =10!(1+10)−1=11!−1 [proved]
$$\mathrm{1}×\mathrm{1}!+\mathrm{2}×\mathrm{2}!+\mathrm{3}×\mathrm{3}!+…+\mathrm{10}×\mathrm{10}!\:+\mathrm{1}−\mathrm{1} \\ $$$$=\mathrm{2}+\mathrm{2}×\mathrm{2}!+\mathrm{3}×\mathrm{3}!+…+\mathrm{10}×\mathrm{10}!−\mathrm{1} \\ $$$$=\mathrm{2}!\left(\mathrm{1}+\mathrm{2}\right)+\mathrm{3}×\mathrm{3}!+\mathrm{4}×\mathrm{4}!+…+\mathrm{10}×\mathrm{10}!−\mathrm{1} \\ $$$$=\mathrm{3}!+\mathrm{3}×\mathrm{3}!+\mathrm{4}×\mathrm{4}!+…+\mathrm{10}×\mathrm{10}!−\mathrm{1} \\ $$$$=\mathrm{3}!\left(\mathrm{1}+\mathrm{3}\right)+\mathrm{4}×\mathrm{4}!+…+\mathrm{10}×\mathrm{10}!−\mathrm{1} \\ $$$$=\mathrm{4}!\left(\mathrm{1}+\mathrm{4}\right)+\mathrm{5}×\mathrm{5}!+…+\mathrm{10}×\mathrm{10}!−\mathrm{1} \\ $$$$=\mathrm{5}!\left(\mathrm{1}+\mathrm{5}\right)+…+\mathrm{10}×\mathrm{10}!−\mathrm{1} \\ $$$$=… \\ $$$$=\mathrm{10}!\left(\mathrm{1}+\mathrm{10}\right)−\mathrm{1}=\mathrm{11}!−\mathrm{1}\:\left[{proved}\right] \\ $$
Answered by puissant last updated on 05/Oct/21
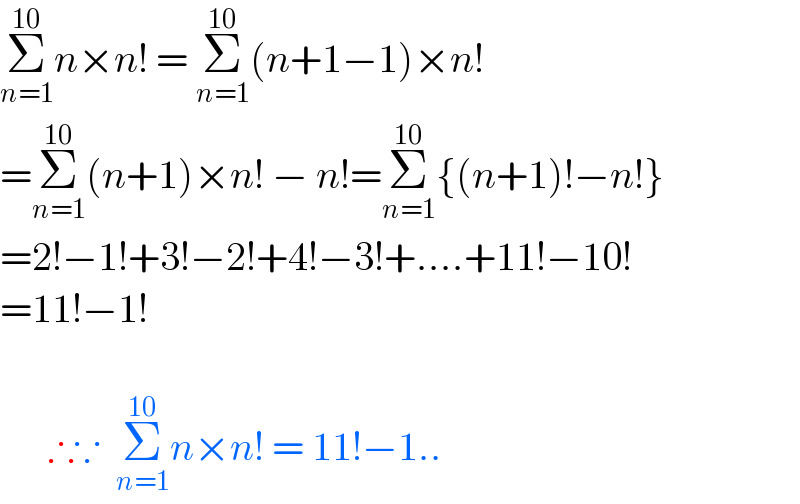
Σ_(n=1) ^(10) n×n! = Σ_(n=1) ^(10) (n+1−1)×n! =Σ_(n=1) ^(10) (n+1)×n! − n!=Σ_(n=1) ^(10) {(n+1)!−n!} =2!−1!+3!−2!+4!−3!+....+11!−10! =11!−1! ∴∵ Σ_(n=1) ^(10) n×n! = 11!−1..
$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{n}×{n}!\:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left({n}+\mathrm{1}−\mathrm{1}\right)×{n}! \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left({n}+\mathrm{1}\right)×{n}!\:−\:{n}!=\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left\{\left({n}+\mathrm{1}\right)!−{n}!\right\} \\ $$$$=\mathrm{2}!−\mathrm{1}!+\mathrm{3}!−\mathrm{2}!+\mathrm{4}!−\mathrm{3}!+….+\mathrm{11}!−\mathrm{10}! \\ $$$$=\mathrm{11}!−\mathrm{1}! \\ $$$$ \\ $$$$\:\:\:\:\:\:\therefore\because\:\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{n}×{n}!\:=\:\mathrm{11}!−\mathrm{1}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *