Question Number 148270 by abdurehime last updated on 26/Jul/21
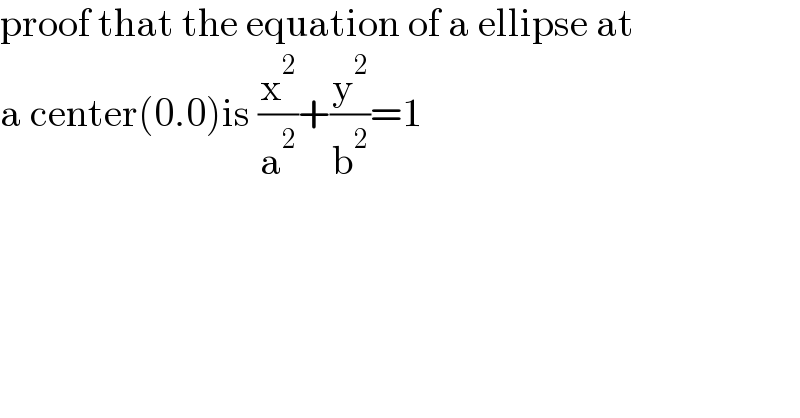
$$\mathrm{proof}\:\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\:\mathrm{ellipse}\:\mathrm{at} \\ $$$$\mathrm{a}\:\mathrm{center}\left(\mathrm{0}.\mathrm{0}\right)\mathrm{is}\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }=\mathrm{1} \\ $$
Commented by abdurehime last updated on 26/Jul/21

$$\mathrm{i}\:\mathrm{want}\:\mathrm{the}\:\mathrm{process}\:\mathrm{of}\:\mathrm{proof} \\ $$
Answered by Olaf_Thorendsen last updated on 26/Jul/21
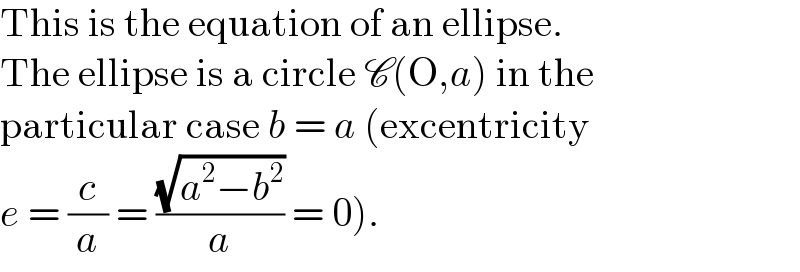
$$\mathrm{This}\:\mathrm{is}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{an}\:\mathrm{ellipse}. \\ $$$$\mathrm{The}\:\mathrm{ellipse}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle}\:\mathscr{C}\left(\mathrm{O},{a}\right)\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{particular}\:\mathrm{case}\:{b}\:=\:{a}\:\left(\mathrm{excentricity}\right. \\ $$$$\left.{e}\:=\:\frac{{c}}{{a}}\:=\:\frac{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}{{a}}\:=\:\mathrm{0}\right). \\ $$
Commented by abdurehime last updated on 26/Jul/21

$$\mathrm{yes}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}!\:\:\:\:\mathrm{sorry} \\ $$
