Menu Close

Proove-that-2-3-2-6-2-4-

Tinku Tara 0 Comments
Pin




Question Number 85649 by Hassen_Timol last updated on 23/Mar/20
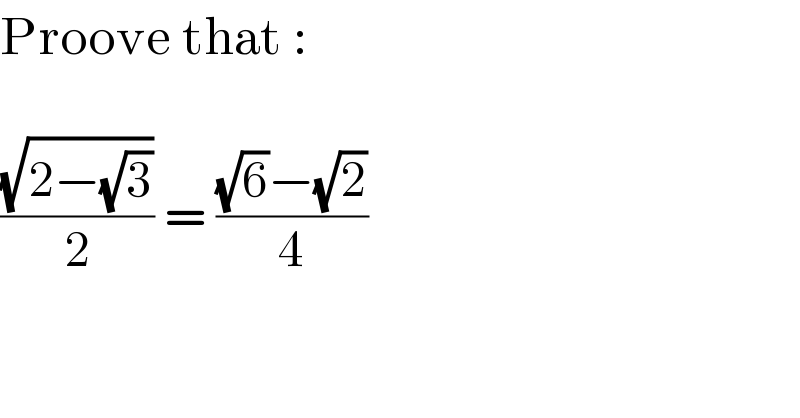
Proove that : ((√(2−(√3)))/2) = (((√6)−(√2))/4)
$$\mathrm{Proove}\:\mathrm{that}\:: \\ $$$$ \\ $$$$\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\:=\:\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 23/Mar/20
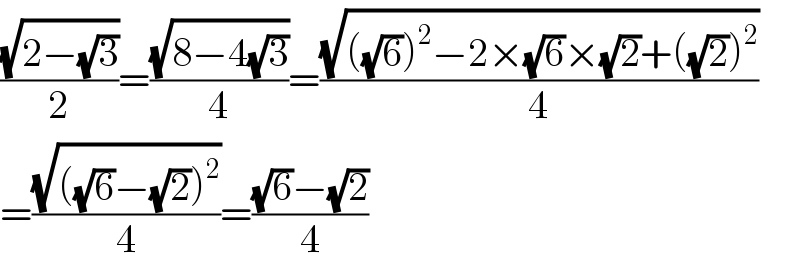
((√(2−(√3)))/2)=((√(8−4(√3)))/4)=((√(((√6))^2 −2×(√6)×(√2)+((√2))^2 ))/4) =((√(((√6)−(√2))^2 ))/4)=(((√6)−(√2))/4)
$$\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}}}{\mathrm{4}}=\frac{\sqrt{\left(\sqrt{\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{2}×\sqrt{\mathrm{6}}×\sqrt{\mathrm{2}}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$=\frac{\sqrt{\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}{\mathrm{4}}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
Answered by MJS last updated on 23/Mar/20
2(√(2−(√3)))=(√6)−(√2) square both sides 4(2−(√3))=((√6)−(√2))^2 8−4(√3)=6−2(√(12))+2 8−4(√3)=8−2(√(2^2 3)) 8−4(√3)=8−4(√3) or: (√(2−(√3)))=a+b(√3) squaring 2−(√3)=a^2 +3b^2 +2ab(√3) ⇒ 2=a^2 +3b^2 ∧−1=2ab ⇒ 2=a^2 +3b^2 ∧b=−(1/(2a)) ⇒ 2=a^2 +(3/(4a^2 )) ⇒ a^4 −2a^2 +(3/4)=0 ⇒ ⇒ a_(1, 2) =±((√2)/2)∨a_(3, 4) =±((√6)/2) ⇒ b_j =−a_j ⇒ (√(2−(√3)))=a_j −a_j (√3)=±(((√6)/2)−((√2)/2)) but we know (√(2−(√3)))>0 ⇒ (√(2−(√3)))=((√6)/2)−((√2)/2) and ((√(2−(√3)))/2)=(((√6)−(√2))/4)
$$\mathrm{2}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}=\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{square}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\mathrm{4}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)=\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}=\mathrm{6}−\mathrm{2}\sqrt{\mathrm{12}}+\mathrm{2} \\ $$$$\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}=\mathrm{8}−\mathrm{2}\sqrt{\mathrm{2}^{\mathrm{2}} \mathrm{3}} \\ $$$$\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}=\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{or}: \\ $$$$\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}={a}+{b}\sqrt{\mathrm{3}} \\ $$$$\mathrm{squaring} \\ $$$$\mathrm{2}−\sqrt{\mathrm{3}}={a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{ab}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{2}={a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \wedge−\mathrm{1}=\mathrm{2}{ab} \\ $$$$\Rightarrow\:\mathrm{2}={a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \wedge{b}=−\frac{\mathrm{1}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\:\mathrm{2}={a}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}{a}^{\mathrm{2}} }\:\Rightarrow\:{a}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:{a}_{\mathrm{1},\:\mathrm{2}} =\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\vee{a}_{\mathrm{3},\:\mathrm{4}} =\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\:\Rightarrow\:{b}_{{j}} =−{a}_{{j}} \\ $$$$\Rightarrow\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}={a}_{{j}} −{a}_{{j}} \sqrt{\mathrm{3}}=\pm\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{know}\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}>\mathrm{0}\:\Rightarrow \\ $$$$\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{and} \\ $$$$\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *