Question Number 37218 by Rio Mike last updated on 10/Jun/18
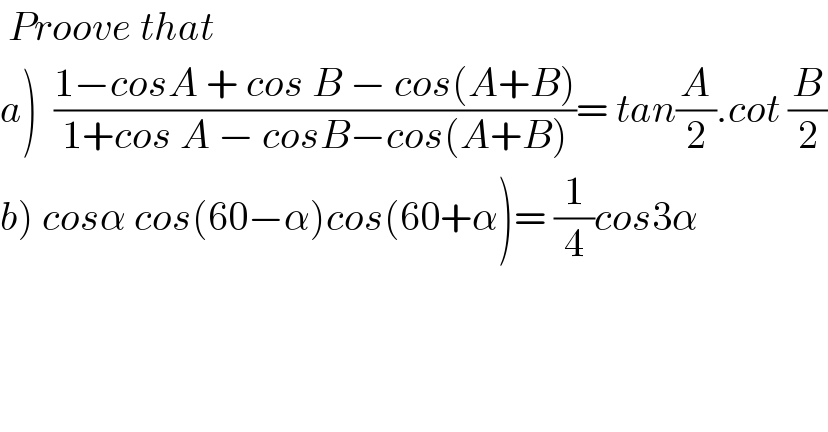
$$\:{Proove}\:{that} \\ $$$$\left.{a}\right)\:\:\frac{\mathrm{1}−{cosA}\:+\:{cos}\:{B}\:−\:{cos}\left({A}+{B}\right)}{\mathrm{1}+{cos}\:{A}\:−\:{cosB}−{cos}\left({A}+{B}\right)}=\:{tan}\frac{{A}}{\mathrm{2}}.{cot}\:\frac{{B}}{\mathrm{2}} \\ $$$$\left.{b}\right)\:{cos}\alpha\:{cos}\left(\mathrm{60}−\alpha\right){cos}\left(\mathrm{60}+\alpha\right)=\:\frac{\mathrm{1}}{\mathrm{4}}{cos}\mathrm{3}\alpha \\ $$$$ \\ $$
Answered by $@ty@m last updated on 11/Jun/18

$$\left({a}\right)\:\:{L}.{H}.{S}. \\ $$$$=\frac{\mathrm{1}−{cosA}\:+\:{cos}\:{B}\:−\:{cos}\left({A}+{B}\right)}{\mathrm{1}+{cos}\:{A}\:−\:{cosB}−{cos}\left({A}+{B}\right)} \\ $$$$=\frac{\mathrm{1}−\mathrm{2sin}\:\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{sin}\:\:\frac{{B}−{A}}{\mathrm{2}}−\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} \frac{{A}+{B}}{\mathrm{2}}}{\mathrm{1}+\mathrm{2sin}\:\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{sin}\:\:\frac{{B}−{A}}{\mathrm{2}}−\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} \frac{{A}+{B}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{sin}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{sin}\:\frac{{A}+{B}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{B}−{A}}{\mathrm{2}}+\mathrm{sin}\:\frac{{A}+{B}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2sin}\:\frac{{A}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}}{\mathrm{2sin}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}}{\mathrm{2}}} \\ $$$$=\mathrm{tan}\:\frac{{A}}{\mathrm{2}}\mathrm{cot}\:\frac{{B}}{\mathrm{2}} \\ $$$$={R}.{H}.{S}. \\ $$$$\left({b}\right)\:\:{L}.{H}.{S}. \\ $$$$=\:{cos}\alpha\:{cos}\left(\mathrm{60}−\alpha\right){cos}\left(\mathrm{60}+\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{cos}\alpha.\mathrm{2}{cos}\left(\mathrm{60}−\alpha\right){cos}\left(\mathrm{60}+\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{cos}\alpha.\left(\mathrm{cos}\:\mathrm{120}+\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{cos}\alpha.\left(−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2cos}\:^{\mathrm{2}} \alpha−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{cos}\alpha.\left(\mathrm{2cos}\:^{\mathrm{2}} \alpha−\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}.\left(\mathrm{4cos}\:^{\mathrm{3}} \alpha−\mathrm{3cos}\:\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{3}\alpha \\ $$$$={R}.{H}.{S}. \\ $$$$ \\ $$
