Question Number 166082 by mnjuly1970 last updated on 12/Feb/22
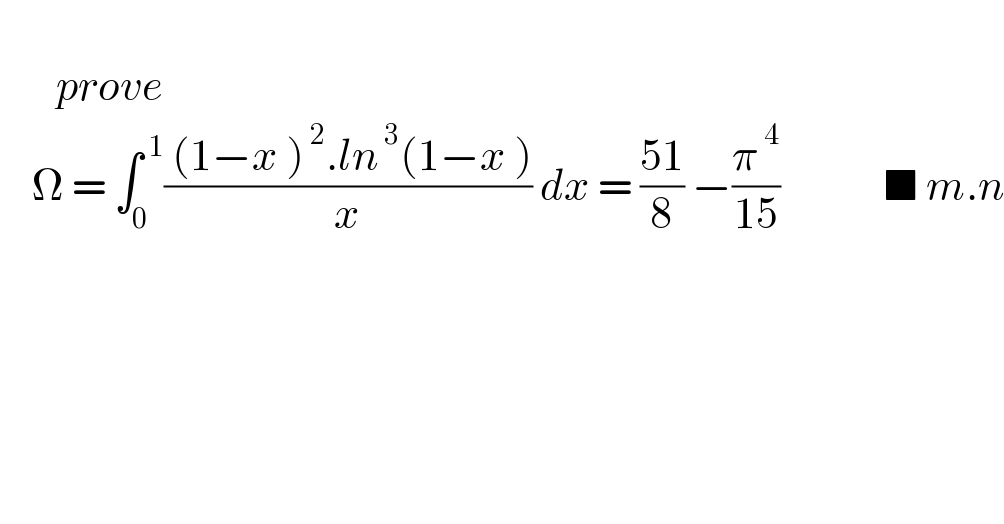
$$ \\ $$$$\:\:\:\:\:\:\:{prove} \\ $$$$\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\left(\mathrm{1}−{x}\:\right)^{\:\mathrm{2}} .{ln}^{\:\mathrm{3}} \left(\mathrm{1}−{x}\:\right)}{{x}}\:{dx}\:=\:\frac{\mathrm{51}}{\mathrm{8}}\:−\frac{\pi^{\:\mathrm{4}} }{\mathrm{15}}\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare\:{m}.{n} \\ $$$$\:\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by qaz last updated on 13/Feb/22
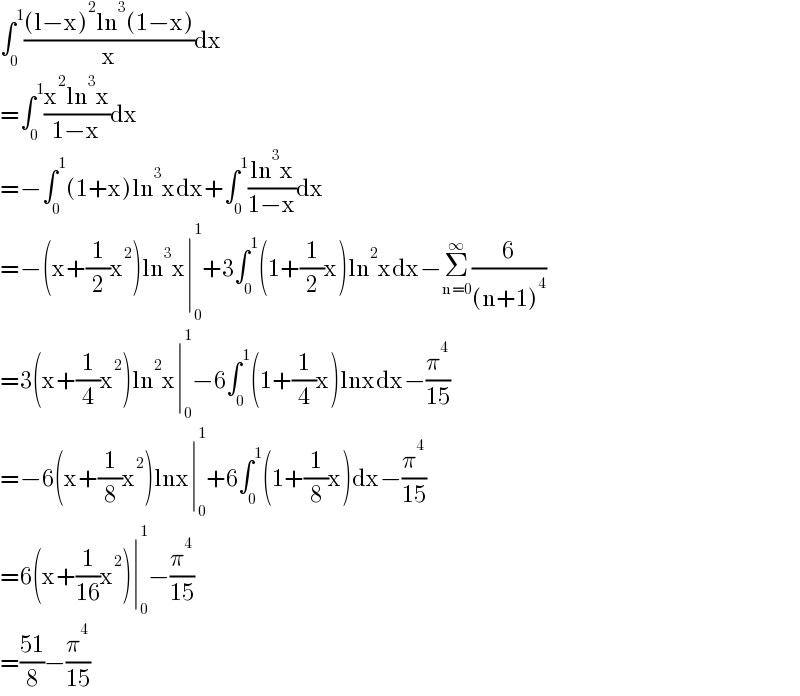
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{l}−\mathrm{x}\right)^{\mathrm{2}} \mathrm{ln}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}^{\mathrm{3}} \mathrm{xdx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=−\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\mathrm{ln}^{\mathrm{3}} \mathrm{x}\mid_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{xdx}−\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{6}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{3}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} \right)\mathrm{ln}^{\mathrm{2}} \mathrm{x}\mid_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{6}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}\right)\mathrm{lnxdx}−\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$$$=−\mathrm{6}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} \right)\mathrm{lnx}\mid_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{6}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}\right)\mathrm{dx}−\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$$$=\mathrm{6}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} −\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$$$=\frac{\mathrm{51}}{\mathrm{8}}−\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$
Commented by mnjuly1970 last updated on 13/Feb/22

$${thx}\:{alot}\:{sir}\:{qaz} \\ $$
