Question Number 154469 by mnjuly1970 last updated on 18/Sep/21
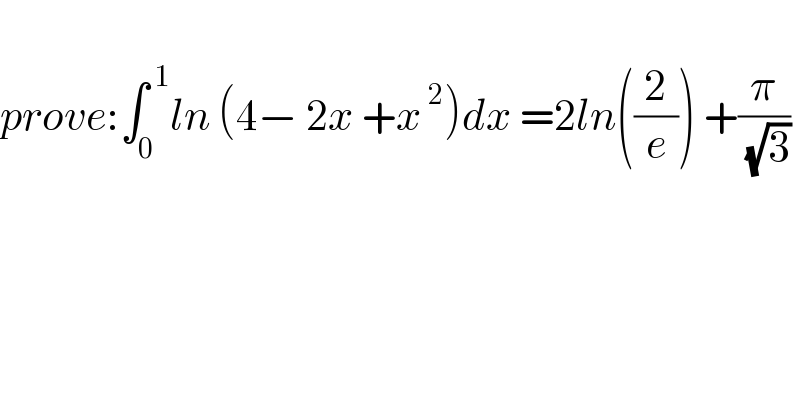
$$ \\ $$$${prove}:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\:\left(\mathrm{4}−\:\mathrm{2}{x}\:+{x}^{\:\mathrm{2}} \right){dx}\:=\mathrm{2}{ln}\left(\frac{\mathrm{2}}{{e}}\right)\:+\frac{\pi}{\:\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Answered by ARUNG_Brandon_MBU last updated on 18/Sep/21
![I=∫_0 ^1 ln(4−2x+x^2 )dx=∫_0 ^1 ln(3+(1−x)^2 )dx =∫_0 ^1 ln(3+x^2 )dx=[xln(3+x^2 )]_0 ^1 −∫_0 ^1 ((2x^2 )/(x^2 +3))dx =ln4−2∫_0 ^1 (1−(3/(x^2 +3)))dx=2ln2−2+2(√3)[tan^(−1) ((x/( (√3))))]_0 ^1 =2ln2−2lne+((√3)/3)π=2ln((2/e))+(π/( (√3)))](https://www.tinkutara.com/question/Q154473.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{4}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{3}+\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \right){dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right){dx}=\left[{x}\mathrm{ln}\left(\mathrm{3}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$$$\:\:=\mathrm{ln4}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{3}}{{x}^{\mathrm{2}} +\mathrm{3}}\right){dx}=\mathrm{2ln2}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:=\mathrm{2ln2}−\mathrm{2ln}{e}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\pi=\mathrm{2ln}\left(\frac{\mathrm{2}}{{e}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}} \\ $$
Commented by mnjuly1970 last updated on 18/Sep/21
$$\:\:{grateful}..{very}\:{nice}\:{solution}.. \\ $$
