Menu Close

prove-0-a-ln-1-ax-1-x-2-dx-1-2-ln-1-a-2-tan-1-a-a-gt-0-

Tinku Tara 0 Comments
Pin




Question Number 98677 by PRITHWISH SEN 2 last updated on 15/Jun/20
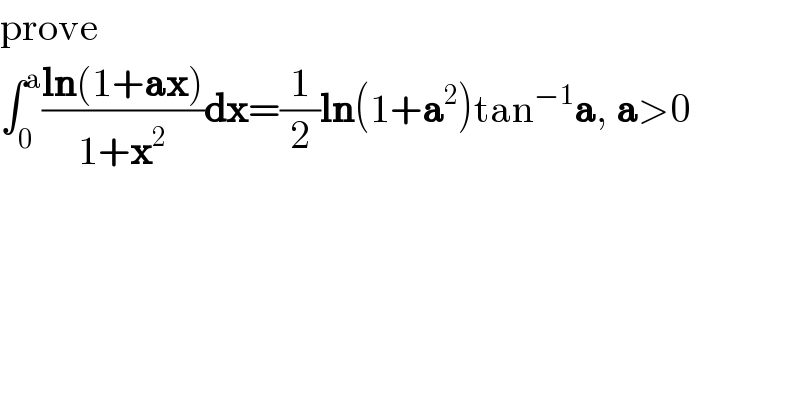
prove ∫_0 ^a ((ln(1+ax))/(1+x^2 ))dx=(1/2)ln(1+a^2 )tan^(−1) a, a>0
$$\mathrm{prove} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{a}} \frac{\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{ax}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\boldsymbol{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)\mathrm{tan}^{−\mathrm{1}} \boldsymbol{\mathrm{a}},\:\boldsymbol{\mathrm{a}}>\mathrm{0} \\ $$
Answered by maths mind last updated on 15/Jun/20
f(t)=∫_0 ^a ((ln(1+tx))/((1+x^2 ))) f′(t)=∫_0 ^a ((xdx)/((1+tx)(1+x^2 ))) =∫_0 ^a (((x+t)(1+tx)−t(1+x^2 ))/((1+t^2 )(1+tx)(1+x^2 ))) =∫_0 ^a ((x+t)/((1+t^2 )(1+x^2 )))dx−∫_0 ^a ((tdx)/((1+t^2 )(1+tx))) =((ln(1+a^2 ))/(2(1+t^2 )))+((tarctan(a))/(t^2 +1))−((ln(1+ta))/(1+t^2 )) f(0)=0 f(a)=∫_0 ^a ((ln(1+ta))/(1+t^2 ))dt f(a)=∫_0 ^a f(t)dt⇒f(a)=∫(((ln(1+a^2 ))/(2(1+t^2 )))+(t/(t^2 +1))arctan(a)−((ln(1+ta))/(1+t^2 )))dt ⇒2f(a)=∫_0 ^a (((ln(1+a^2 ))/(2(1+t^2 )))+(t/(t^2 +1))arctan(a))dt =((ln(1+a^2 ))/2)arctan(a)+((arctan(a))/2)ln(1+a^2 ) ⇔f(a)=((ln(1+a^2 ))/2)tan^(−1) (a)
$${f}\left({t}\right)=\int_{\mathrm{0}} ^{{a}} \frac{{ln}\left(\mathrm{1}+{tx}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{{a}} \frac{{xdx}}{\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \frac{\left({x}+{t}\right)\left(\mathrm{1}+{tx}\right)−{t}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{tx}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{0}} ^{{a}} \frac{{x}+{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}−\int_{\mathrm{0}} ^{{a}} \frac{{tdx}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{tx}\right)} \\ $$$$=\frac{{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{{tarctan}\left({a}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}−\frac{{ln}\left(\mathrm{1}+{ta}\right)}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{{a}} \frac{{ln}\left(\mathrm{1}+{ta}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{{a}} {f}\left({t}\right){dt}\Rightarrow{f}\left({a}\right)=\int\left(\frac{{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{arctan}\left({a}\right)−\frac{{ln}\left(\mathrm{1}+{ta}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt} \\ $$$$\Rightarrow\mathrm{2}{f}\left({a}\right)=\int_{\mathrm{0}} ^{{a}} \left(\frac{{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{arctan}\left({a}\right)\right){dt} \\ $$$$=\frac{{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}{\mathrm{2}}{arctan}\left({a}\right)+\frac{{arctan}\left({a}\right)}{\mathrm{2}}{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow{f}\left({a}\right)=\frac{{ln}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left({a}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 16/Jun/20
thank you sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *