Menu Close

prove-0-ln-2-x-ln-1-x-2-1-x-2-dx-7pi-4-3-pi-3-ln-2-4-where-3-is-a-pery-s-constant-

Tinku Tara 0 Comments
Pin




Question Number 130254 by Eric002 last updated on 23/Jan/21
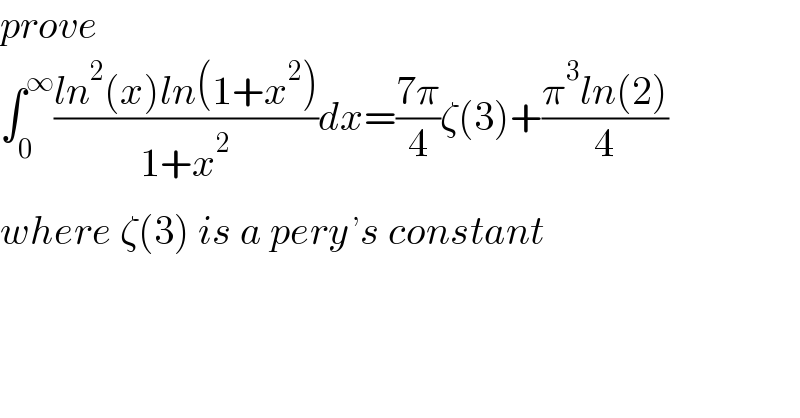
prove ∫_0 ^∞ ((ln^2 (x)ln(1+x^2 ))/(1+x^2 ))dx=((7π)/4)ζ(3)+((π^3 ln(2))/4) where ζ(3) is a pery^( ,) s constant
$${prove} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{7}\pi}{\mathrm{4}}\zeta\left(\mathrm{3}\right)+\frac{\pi^{\mathrm{3}} {ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$${where}\:\zeta\left(\mathrm{3}\right)\:{is}\:{a}\:{pery}^{\:,} {s}\:{constant} \\ $$
Answered by mindispower last updated on 26/Jan/21
∫_0 ^(π/2) (ln^2 (sin(x))+ln^2 (cos^2 (x))−2ln(sin(x))ln(cos(x)).ln((1/(cos^2 (x))))dx =−2∫_0 ^(π/2) ln^2 (sin(x))ln(cos(x))dx−2∫_0 ^(π/2) ln^3 (cos(x))dx +4∫_0 ^(π/2) ln^2 (cos(x))ln(sin(x))dx=−2A−2B+4C recall β(a,b)=2∫_0 ^(π/2) cos^(2a−1) (x)sin^(2b−1) (x)dx (∂^3 /(∂^2 b∂a))β((1/2),(1/2))=8A,(∂^3 /(∂^2 a∂b))β((1/2),(1/2))=8C ((∂^3 β((1/2),(1/2)))/∂^3 a)=8B ∂_a β(a,b)=β(a,b)(Ψ(a)−Ψ(a+b)) ∂_a ^2 β(a,b)=β(a,b)(Ψ(a)−Ψ(a+b)^2 +(Ψ′(a)−Ψ′(a+b))β(a,b) ∂_a ^2 ∂_b β(a,b)=β(a,b)(Ψ(b)−Ψ(a+b))(Ψ(a)−Ψ(a+b))^2 −2Ψ′(a+b)(Ψ(a)−Ψ(a+b))(Ψ(a)−Ψ(a+b))β(a,b) +β(a,b)(Ψ(b)−Ψ(a+b)))(Ψ′(a)−Ψ′(a+b)) −Ψ′′(a+b)β(a,b)) ∂^2 a∂bβ((1/2_ ),(1/2)) i will finish?it later Ψ((1/2)) can easly valuted Ψ′(1)=ζ(2)=(π^2 /6)...=
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({ln}^{\mathrm{2}} \left({sin}\left({x}\right)\right)+{ln}^{\mathrm{2}} \left({cos}^{\mathrm{2}} \left({x}\right)\right)−\mathrm{2}{ln}\left({sin}\left({x}\right)\right){ln}\left({cos}\left({x}\right)\right).{ln}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)}\right){dx}\right. \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}^{\mathrm{2}} \left({sin}\left({x}\right)\right){ln}\left({cos}\left({x}\right)\right){dx}−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}^{\mathrm{3}} \left({cos}\left({x}\right)\right){dx} \\ $$$$+\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}^{\mathrm{2}} \left({cos}\left({x}\right)\right){ln}\left({sin}\left({x}\right)\right){dx}=−\mathrm{2}{A}−\mathrm{2}{B}+\mathrm{4}{C} \\ $$$${recall} \\ $$$$\beta\left({a},{b}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{a}−\mathrm{1}} \left({x}\right){sin}^{\mathrm{2}{b}−\mathrm{1}} \left({x}\right){dx} \\ $$$$\frac{\partial^{\mathrm{3}} }{\partial^{\mathrm{2}} {b}\partial{a}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{8}{A},\frac{\partial^{\mathrm{3}} }{\partial^{\mathrm{2}} {a}\partial{b}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{8}{C} \\ $$$$\frac{\partial^{\mathrm{3}} \beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)}{\partial^{\mathrm{3}} {a}}=\mathrm{8}{B} \\ $$$$\partial_{{a}} \beta\left({a},{b}\right)=\beta\left({a},{b}\right)\left(\Psi\left({a}\right)−\Psi\left({a}+{b}\right)\right) \\ $$$$\partial_{{a}} ^{\mathrm{2}} \beta\left({a},{b}\right)=\beta\left({a},{b}\right)\left(\Psi\left({a}\right)−\Psi\left({a}+{b}\right)^{\mathrm{2}} +\left(\Psi'\left({a}\right)−\Psi'\left({a}+{b}\right)\right)\beta\left({a},{b}\right)\right. \\ $$$$\partial_{{a}} ^{\mathrm{2}} \partial_{{b}} \beta\left({a},{b}\right)=\beta\left({a},{b}\right)\left(\Psi\left({b}\right)−\Psi\left({a}+{b}\right)\right)\left(\Psi\left({a}\right)−\Psi\left({a}+{b}\right)\right)^{\mathrm{2}} \\ $$$$−\mathrm{2}\Psi'\left({a}+{b}\right)\left(\Psi\left({a}\right)−\Psi\left({a}+{b}\right)\right)\left(\Psi\left({a}\right)−\Psi\left({a}+{b}\right)\right)\beta\left({a},{b}\right) \\ $$$$\left.+\beta\left({a},{b}\right)\left(\Psi\left({b}\right)−\Psi\left({a}+{b}\right)\right)\right)\left(\Psi'\left({a}\right)−\Psi'\left({a}+{b}\right)\right) \\ $$$$\left.−\Psi''\left({a}+{b}\right)\beta\left({a},{b}\right)\right) \\ $$$$\partial^{\mathrm{2}} {a}\partial{b}\beta\left(\frac{\mathrm{1}}{\mathrm{2}_{} },\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${i}\:{will}\:{finish}?{it}\:{later} \\ $$$$\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{can}\:{easly}\:{valuted} \\ $$$$\Psi'\left(\mathrm{1}\right)=\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}…= \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *