Question Number 164547 by mnjuly1970 last updated on 21/Jan/22
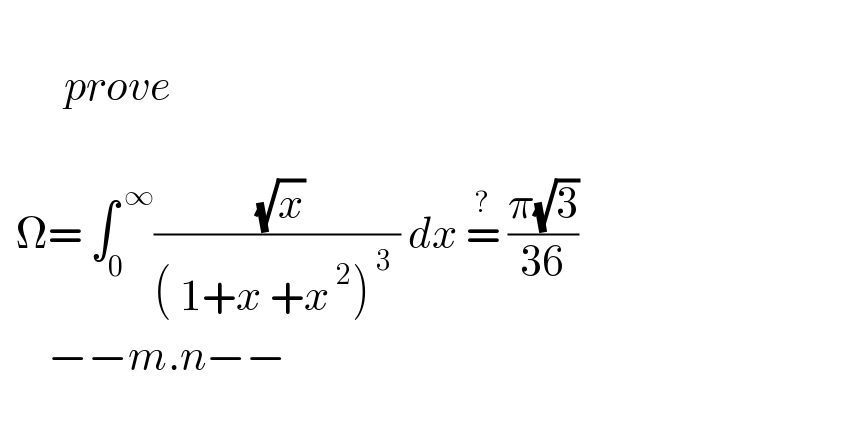
$$ \\ $$$$\:\:\:\:\:\:\:\:{prove} \\ $$$$\: \\ $$$$\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:\sqrt{{x}}}{\left(\:\mathrm{1}+{x}\:+{x}^{\:\mathrm{2}} \right)^{\:\mathrm{3}} \:}\:{dx}\:\overset{?} {=}\:\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{36}}\: \\ $$$$\:\:\:\:\:\:−−{m}.{n}−−\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 19/Jan/22
![∫((√x)/((x^2 +x+2)^3 ))dx= [t=(√x) → dx=2(√x)dt] =2∫(t^2 /((t^4 +t^2 +1)^3 ))dt= [Ostrogradski′s Method] =((t(7t^6 +10t^4 +14t^2 +5))/(12(t^4 +t^2 +1)^2 ))+(1/(12))∫((7t^2 −5)/(t^4 +t^2 +1))dt= (1/(12))∫((7t^2 −5)/(t^4 +t^2 +1))dt= =(1/4)∫((2t−1)/(t^2 −t+1))dt+(1/(24))∫(dt/(t^2 −t+1))−(1/4)∫((2t+1)/(t^2 +t+1))dt+(1/(24))∫(dt/(t^2 +t+1))= ... =(1/4)ln ((t^2 −t+1)/(t^2 +t+1)) +((√3)/(36))(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3)) =((t(7t^6 +10t^4 +14t^2 +5))/(12(t^4 +t^2 +1)^2 ))+(1/4)ln ((t^2 −t+1)/(t^2 +t+1)) +((√3)/(36))(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3))= =(((√x)(7x^3 +10x^2 +14x+5))/(12(x^2 +x+1)^2 ))+(1/4)ln ((x−(√x)+1)/(x+(√x)+1)) +((√3)/(36))(arctan (((√3)(2(√x)−1))/3) +arctan (((√3)(2(√x)+1))/3))+C ⇒ ∫_0 ^∞ ((√x)/((x^2 +x+2)^3 ))dx=(((√3)π)/(36))](https://www.tinkutara.com/question/Q164566.png)
$$\int\frac{\sqrt{{x}}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{{t}\left(\mathrm{7}{t}^{\mathrm{6}} +\mathrm{10}{t}^{\mathrm{4}} +\mathrm{14}{t}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{12}\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{7}{t}^{\mathrm{2}} −\mathrm{5}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$ \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{7}{t}^{\mathrm{2}} −\mathrm{5}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt}+\frac{\mathrm{1}}{\mathrm{24}}\int\frac{{dt}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}+\frac{\mathrm{1}}{\mathrm{24}}\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}= \\ $$$$\:\:\:\:\:… \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}}\right) \\ $$$$ \\ $$$$=\frac{{t}\left(\mathrm{7}{t}^{\mathrm{6}} +\mathrm{10}{t}^{\mathrm{4}} +\mathrm{14}{t}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{12}\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}}\right)= \\ $$$$=\frac{\sqrt{{x}}\left(\mathrm{7}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{5}\right)}{\mathrm{12}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{{x}−\sqrt{{x}}+\mathrm{1}}{{x}+\sqrt{{x}}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}\sqrt{{x}}−\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}\sqrt{{x}}+\mathrm{1}\right)}{\mathrm{3}}\right)+{C} \\ $$$$ \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\sqrt{{x}}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{2}\right)^{\mathrm{3}} }{dx}=\frac{\sqrt{\mathrm{3}}\pi}{\mathrm{36}} \\ $$
