Menu Close

prove-1-11-111-111-111-n-times-10-n-1-9n-10-81-

Tinku Tara 0 Comments
Pin




Question Number 44716 by Tawa1 last updated on 03/Oct/18
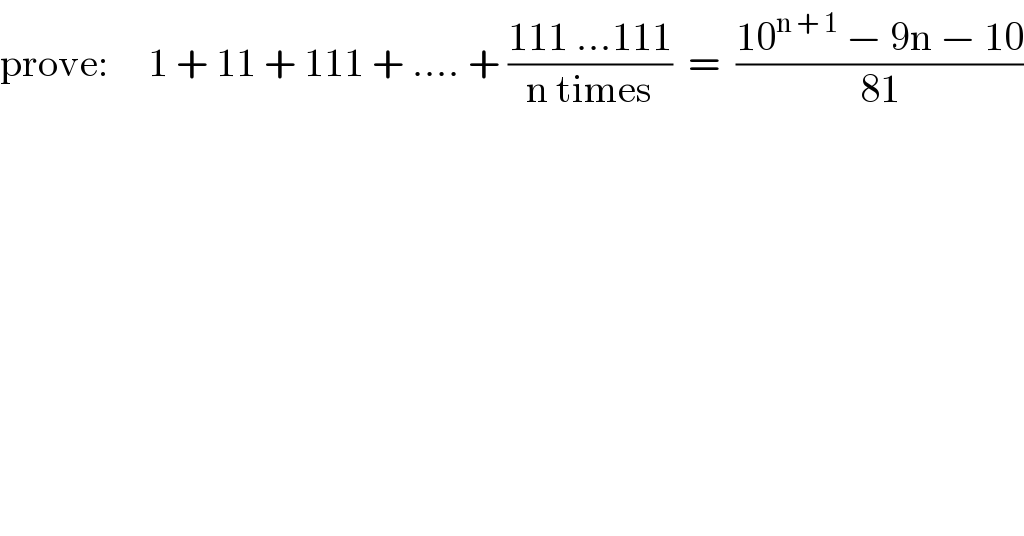
prove: 1 + 11 + 111 + .... + ((111 ...111)/(n times)) = ((10^(n + 1) − 9n − 10)/(81))
$$\mathrm{prove}:\:\:\:\:\:\mathrm{1}\:+\:\mathrm{11}\:+\:\mathrm{111}\:+\:….\:+\:\frac{\mathrm{111}\:…\mathrm{111}}{\mathrm{n}\:\mathrm{times}}\:\:=\:\:\frac{\mathrm{10}^{\mathrm{n}\:+\:\mathrm{1}} \:−\:\mathrm{9n}\:−\:\mathrm{10}}{\mathrm{81}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Oct/18
s=1+11+111+1111+...+111..._(n times) 111 9s=9+99+999+9999+...+999...999 9s=(10−1)+(10^2 −1)+(10^3 −1)+(10^4 −1)+..+(10^n −1) 9s=(10+10^2 +10^3 +..+10^n )−(1+1+1...ntimes) 9s=((10(10^n −1))/(10−1))−n s=((10^(n+1) −10−9n)/(81)) proof by mathematical induction step 1 put n=1 right hand side obtained value in RHS is ((10^2 −10−9×1)/(81))=1 now in LHS value also 1 so given statement is true for n=1 step 2 put n=2 RHS=((10^(2+1) −10−9×2)/(81))=((1000−10−18)/(81))=12 LHS is also 1+11=12 so for n= 2 it is true step 3 let we assume for n=m it is true then we have to prove that it is true for m+1 1+11+111+...+111..111←m times=((10^(m+1) −10−9m)/(81)) now add 111...111 ←(m+1)tkmes in LHS ((10^(m+1) −10−9m)/(81))+111...111←(m+1)times =((10^(m+1) −10−9m)/(81))+(1/9)(999...999)←(m+1)times =((10^(m+1) −10−9m)/(81))+(1/9)(10^(m+1) −1) =((10^(m+1) −10−9m+9(10^(m+1) −1))/(81)) =((10^(m+1) −10−9m+(10−1)(10^(m+1) −1))/(81)) =((10^(m+1) −10−9m+10^(m+2) −10−10^(m+1) +1)/(81)) =((10^(m+2) −10−9m−10+1)/(81)) =((10^(m+2) −10−9m−9)/(81)) =((10^(m+2) −10−9(m+1))/(81)) if you put n=m+1 RHS ((10^(m+2) −10−9(m+1))/(81)) so given statement aso true for m+1 so it true for m qnd m+1...
$${s}=\mathrm{1}+\mathrm{11}+\mathrm{111}+\mathrm{1111}+…+\mathrm{111}..\underset{{n}\:{times}} {.}\mathrm{111} \\ $$$$\mathrm{9}{s}=\mathrm{9}+\mathrm{99}+\mathrm{999}+\mathrm{9999}+…+\mathrm{999}…\mathrm{999} \\ $$$$\mathrm{9}{s}=\left(\mathrm{10}−\mathrm{1}\right)+\left(\mathrm{10}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{10}^{\mathrm{3}} −\mathrm{1}\right)+\left(\mathrm{10}^{\mathrm{4}} −\mathrm{1}\right)+..+\left(\mathrm{10}^{{n}} −\mathrm{1}\right) \\ $$$$\mathrm{9}{s}=\left(\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +..+\mathrm{10}^{{n}} \right)−\left(\mathrm{1}+\mathrm{1}+\mathrm{1}…{ntimes}\right) \\ $$$$\mathrm{9}{s}=\frac{\mathrm{10}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{10}−\mathrm{1}}−{n} \\ $$$${s}=\frac{\mathrm{10}^{{n}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{n}}{\mathrm{81}} \\ $$$${proof}\:{by}\:{mathematical}\:{induction} \\ $$$${step}\:\mathrm{1}\:{put}\:{n}=\mathrm{1}\:{right}\:{hand}\:{side} \\ $$$${obtained}\:{value}\:{in}\:{RHS}\:{is}\:\frac{\mathrm{10}^{\mathrm{2}} −\mathrm{10}−\mathrm{9}×\mathrm{1}}{\mathrm{81}}=\mathrm{1} \\ $$$${now}\:{in}\:{LHS}\:{value}\:{also}\:\mathrm{1} \\ $$$${so}\:{given}\:{statement}\:{is}\:{true}\:{for}\:{n}=\mathrm{1} \\ $$$${step}\:\mathrm{2}\:{put}\:{n}=\mathrm{2} \\ $$$${RHS}=\frac{\mathrm{10}^{\mathrm{2}+\mathrm{1}} −\mathrm{10}−\mathrm{9}×\mathrm{2}}{\mathrm{81}}=\frac{\mathrm{1000}−\mathrm{10}−\mathrm{18}}{\mathrm{81}}=\mathrm{12} \\ $$$${LHS}\:{is}\:{also}\:\mathrm{1}+\mathrm{11}=\mathrm{12}\: \\ $$$${so}\:{for}\:{n}=\:\mathrm{2}\:{it}\:{is}\:{true} \\ $$$${step}\:\mathrm{3} \\ $$$${let}\:{we}\:{assume}\:{for}\:{n}={m}\:{it}\:{is}\:{true}\: \\ $$$${then}\:{we}\:{have}\:{to}\:{prove}\:{that}\:{it}\:{is}\:{true}\:{for}\:{m}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{11}+\mathrm{111}+…+\mathrm{111}..\mathrm{111}\leftarrow{m}\:{times}=\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}}{\mathrm{81}} \\ $$$${now}\:{add}\:\mathrm{111}…\mathrm{111}\:\leftarrow\left({m}+\mathrm{1}\right){tkmes}\:{in}\:{LHS} \\ $$$$ \\ $$$$\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}}{\mathrm{81}}+\mathrm{111}…\mathrm{111}\leftarrow\left({m}+\mathrm{1}\right){times} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}}{\mathrm{81}}+\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{999}…\mathrm{999}\right)\leftarrow\left({m}+\mathrm{1}\right){times} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}}{\mathrm{81}}+\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{1}\right) \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}+\mathrm{9}\left(\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{1}\right)}{\mathrm{81}} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}+\left(\mathrm{10}−\mathrm{1}\right)\left(\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{1}\right)}{\mathrm{81}} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{1}} −\mathrm{10}−\mathrm{9}{m}+\mathrm{10}^{{m}+\mathrm{2}} −\mathrm{10}−\mathrm{10}^{{m}+\mathrm{1}} +\mathrm{1}}{\mathrm{81}} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{2}} −\mathrm{10}−\mathrm{9}{m}−\mathrm{10}+\mathrm{1}}{\mathrm{81}} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{2}} −\mathrm{10}−\mathrm{9}{m}−\mathrm{9}}{\mathrm{81}} \\ $$$$=\frac{\mathrm{10}^{{m}+\mathrm{2}} −\mathrm{10}−\mathrm{9}\left({m}+\mathrm{1}\right)}{\mathrm{81}} \\ $$$${if}\:{you}\:{put}\:{n}={m}+\mathrm{1}\:{RHS} \\ $$$$\frac{\mathrm{10}^{{m}+\mathrm{2}} −\mathrm{10}−\mathrm{9}\left({m}+\mathrm{1}\right)}{\mathrm{81}}\:\:{so}\:{given}\:{statement}\:{aso}\:{true} \\ $$$${for}\:{m}+\mathrm{1}\:\:\: \\ $$$${so}\:{it}\:{true}\:{for}\:{m}\:{qnd}\:{m}+\mathrm{1}… \\ $$$$ \\ $$
Commented by Tawa1 last updated on 03/Oct/18
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 03/Oct/18
Please sir, can you help me to use mathematical induction sir
$$\mathrm{Please}\:\mathrm{sir},\:\mathrm{can}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{use}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Oct/18
yes...
$${yes}… \\ $$
Commented by Tawa1 last updated on 03/Oct/18
God bless you sir. help me to use induction
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{use}\:\mathrm{induction} \\ $$
Commented by Tawa1 last updated on 04/Oct/18
God bless you sir. I really appreciate your effort.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}.\: \\ $$
Commented by Necxx last updated on 04/Oct/18
wow....I′ve also sought the answer for this.Thanks Mr Tanmay.
$${wow}….{I}'{ve}\:{also}\:{sought}\:{the}\:{answer} \\ $$$${for}\:{this}.{Thanks}\:{Mr}\:{Tanmay}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *