Question Number 106816 by bemath last updated on 07/Aug/20

$$\mathrm{prove}\:\mathrm{by}\:\mathrm{mathematical}\:\mathrm{induction} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{n}^{\mathrm{2}} \:\leqslant\:\mathrm{2}^{\mathrm{n}} \:;\:\mathrm{n}\:\geqslant\:\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\:\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:<\:\mathrm{2n}^{\mathrm{2}} \:;\:\mathrm{n}\:\geqslant\:\mathrm{3} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{2}^{\mathrm{n}} −\mathrm{3}\:\geqslant\:\mathrm{2}^{\mathrm{n}−\mathrm{2}} \:;\:\mathrm{n}\:\geqslant\:\mathrm{5} \\ $$$$\:\:\:\:\:\:@\mathrm{bemath}@ \\ $$
Commented by bobhans last updated on 07/Aug/20
![(2)n^2 +2n+1< 2n^2 ; 2n+1 < n^2 ; n≥3 P_1 (n=3)⇒2.3+1<3^2 [ true ] let :P_k (n=k,k≥3)⇒2k+1 < k^2 [true] P_(k+1) (n=k+1)⇒LHS : 2(k+1)+1 = 2k+3 = (2k+1)+2 < k^2 +2 =k^2 −2k+1+(1+2k) =(k+1)^2 +2k+1 =](https://www.tinkutara.com/question/Q106820.png)
$$\left(\mathrm{2}\right)\mathrm{n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1}<\:\mathrm{2n}^{\mathrm{2}} \:;\:\mathrm{2n}+\mathrm{1}\:<\:\mathrm{n}^{\mathrm{2}} \:;\:\mathrm{n}\geqslant\mathrm{3} \\ $$$$\mathrm{P}_{\mathrm{1}} \left(\mathrm{n}=\mathrm{3}\right)\Rightarrow\mathrm{2}.\mathrm{3}+\mathrm{1}<\mathrm{3}^{\mathrm{2}} \:\:\left[\:\mathrm{true}\:\right] \\ $$$$\mathrm{let}\::\mathrm{P}_{\mathrm{k}} \left(\mathrm{n}=\mathrm{k},\mathrm{k}\geqslant\mathrm{3}\right)\Rightarrow\mathrm{2k}+\mathrm{1}\:<\:\mathrm{k}^{\mathrm{2}} \:\:\:\left[\mathrm{true}\right] \\ $$$$\mathrm{P}_{\mathrm{k}+\mathrm{1}} \left(\mathrm{n}=\mathrm{k}+\mathrm{1}\right)\Rightarrow\mathrm{LHS}\::\:\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)+\mathrm{1}\:=\:\mathrm{2k}+\mathrm{3} \\ $$$$=\:\left(\mathrm{2k}+\mathrm{1}\right)+\mathrm{2}\:<\:\mathrm{k}^{\mathrm{2}} +\mathrm{2}\:=\mathrm{k}^{\mathrm{2}} −\mathrm{2k}+\mathrm{1}+\left(\mathrm{1}+\mathrm{2k}\right) \\ $$$$=\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2k}+\mathrm{1}\:=\: \\ $$$$ \\ $$$$ \\ $$
Answered by bobhans last updated on 07/Aug/20
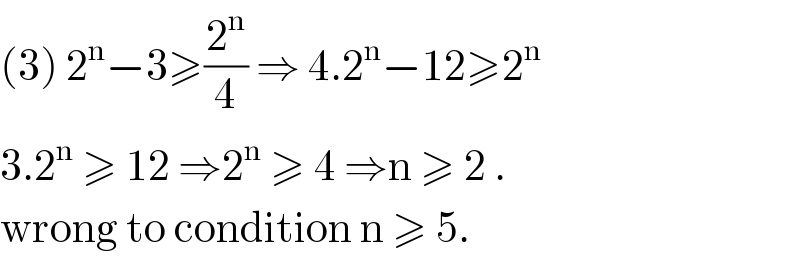
$$\left(\mathrm{3}\right)\:\mathrm{2}^{\mathrm{n}} −\mathrm{3}\geqslant\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{4}}\:\Rightarrow\:\mathrm{4}.\mathrm{2}^{\mathrm{n}} −\mathrm{12}\geqslant\mathrm{2}^{\mathrm{n}} \\ $$$$\mathrm{3}.\mathrm{2}^{\mathrm{n}} \:\geqslant\:\mathrm{12}\:\Rightarrow\mathrm{2}^{\mathrm{n}} \:\geqslant\:\mathrm{4}\:\Rightarrow\mathrm{n}\:\geqslant\:\mathrm{2}\:. \\ $$$$\mathrm{wrong}\:\mathrm{to}\:\mathrm{condition}\:\mathrm{n}\:\geqslant\:\mathrm{5}. \\ $$
Answered by Rio Michael last updated on 07/Aug/20

$$\:\left(\mathrm{1}\right)\:\mathrm{claim}:\:\:{n}^{\mathrm{2}} \:\leqslant\:\mathrm{2}^{{n}} \:;\:\mathrm{if}\:{n}\:\geqslant\:\mathrm{4} \\ $$$$\mathrm{prove}\:\mathrm{for}\:{n}\:=\:\mathrm{4}\:\Rightarrow\:\:\mathrm{4}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{4}} \:=\:\mathrm{16} \\ $$$$\mathrm{prove}\:\mathrm{for}\:{n}\:=\:\mathrm{6}\:\Rightarrow\:\mathrm{6}^{\mathrm{2}} \leqslant\:\mathrm{2}^{\mathrm{6}} \: \\ $$$$\mathrm{Assume}\:\mathrm{that}\:\:{n}\:=\:{k}\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{claim}. \\ $$$$\therefore\:{k}^{\mathrm{2}} \:\leqslant\:\mathrm{2}^{{k}} \::\:\mathrm{if}\:{k}\:\geqslant\:\mathrm{4} \\ $$$$\mathrm{proving}\:\mathrm{for}\:{n}\:=\:{k}+\mathrm{1} \\ $$$$\Rightarrow\:\:\left({k}+\mathrm{1}\right)^{\mathrm{2}} \:\leqslant\:\mathrm{2}^{{k}+\mathrm{1}} \\ $$$$\Rightarrow\:\:{k}^{\mathrm{2}} \:+\:\mathrm{2}{k}\:+\:\mathrm{1}\:\leqslant\:\mathrm{2}\left(\mathrm{2}^{{k}} \right) \\ $$$$\mathrm{but}\:{k}^{\mathrm{2}} \:\leqslant\:\mathrm{2}^{{k}} \:\Rightarrow\:{k}^{\mathrm{2}} \:\leqslant\:\mathrm{2}\left(\mathrm{2}^{{k}} \right) \\ $$$$\mathrm{also}\:\:{k}^{\mathrm{2}} \:\geqslant\:\mathrm{2}{k}\:\forall\:{k}\:\in\:\mathbb{Z}\:\:\: \\ $$$$\mathrm{thus}\:{k}^{\mathrm{2}} \:+\:\mathrm{2}{k}\:+\:\mathrm{1}\:\leqslant\:\mathrm{2}\left(\mathrm{2}^{{k}} \right)\:\mathrm{if}\:\:{k}\:\geqslant\:\mathrm{3} \\ $$
