Menu Close

prove-by-mathematical-induction-2-3-4-3-6-3-8-3-2n-3-2n-2-n-1-2-

Tinku Tara 0 Comments
Pin




Question Number 105605 by bobhans last updated on 30/Jul/20
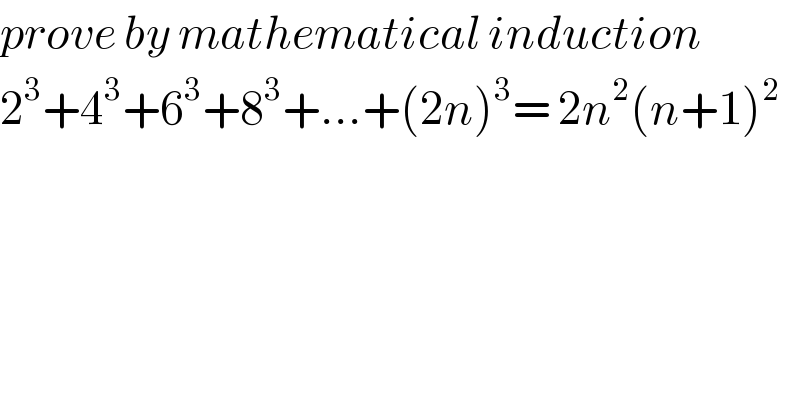
prove by mathematical induction 2^3 +4^3 +6^3 +8^3 +...+(2n)^3 = 2n^2 (n+1)^2
$${prove}\:{by}\:{mathematical}\:{induction}\: \\ $$$$\mathrm{2}^{\mathrm{3}} +\mathrm{4}^{\mathrm{3}} +\mathrm{6}^{\mathrm{3}} +\mathrm{8}^{\mathrm{3}} +…+\left(\mathrm{2}{n}\right)^{\mathrm{3}} =\:\mathrm{2}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$
Answered by bemath last updated on 30/Jul/20
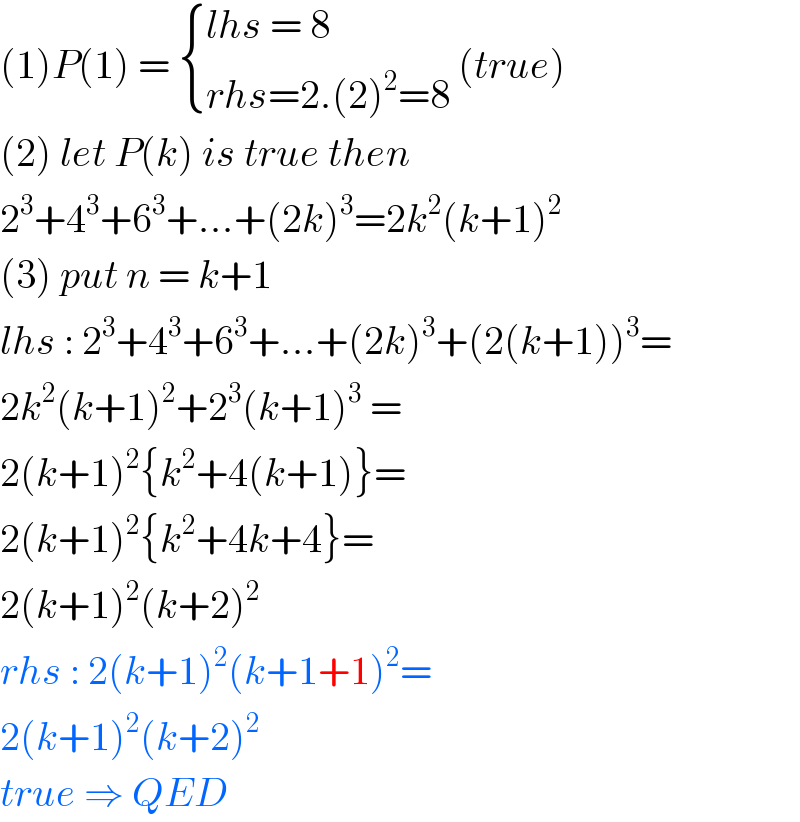
(1)P(1) = { ((lhs = 8)),((rhs=2.(2)^2 =8)) :} (true) (2) let P(k) is true then 2^3 +4^3 +6^3 +...+(2k)^3 =2k^2 (k+1)^2 (3) put n = k+1 lhs : 2^3 +4^3 +6^3 +...+(2k)^3 +(2(k+1))^3 = 2k^2 (k+1)^2 +2^3 (k+1)^3 = 2(k+1)^2 {k^2 +4(k+1)}= 2(k+1)^2 {k^2 +4k+4}= 2(k+1)^2 (k+2)^2 rhs : 2(k+1)^2 (k+1+1)^2 = 2(k+1)^2 (k+2)^2 true ⇒ QED
$$\left(\mathrm{1}\right){P}\left(\mathrm{1}\right)\:=\:\begin{cases}{{lhs}\:=\:\mathrm{8}}\\{{rhs}=\mathrm{2}.\left(\mathrm{2}\right)^{\mathrm{2}} =\mathrm{8}}\end{cases}\:\left({true}\right) \\ $$$$\left(\mathrm{2}\right)\:{let}\:{P}\left({k}\right)\:{is}\:{true}\:{then}\: \\ $$$$\mathrm{2}^{\mathrm{3}} +\mathrm{4}^{\mathrm{3}} +\mathrm{6}^{\mathrm{3}} +…+\left(\mathrm{2}{k}\right)^{\mathrm{3}} =\mathrm{2}{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:{put}\:{n}\:=\:{k}+\mathrm{1} \\ $$$${lhs}\::\:\mathrm{2}^{\mathrm{3}} +\mathrm{4}^{\mathrm{3}} +\mathrm{6}^{\mathrm{3}} +…+\left(\mathrm{2}{k}\right)^{\mathrm{3}} +\left(\mathrm{2}\left({k}+\mathrm{1}\right)\right)^{\mathrm{3}} = \\ $$$$\mathrm{2}{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} \left({k}+\mathrm{1}\right)^{\mathrm{3}} \:= \\ $$$$\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left\{{k}^{\mathrm{2}} +\mathrm{4}\left({k}+\mathrm{1}\right)\right\}= \\ $$$$\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left\{{k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{4}\right\}= \\ $$$$\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left({k}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$${rhs}\::\:\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left({k}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} = \\ $$$$\mathrm{2}\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left({k}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$${true}\:\Rightarrow\:{QED}\: \\ $$
Answered by Dwaipayan Shikari last updated on 30/Jul/20
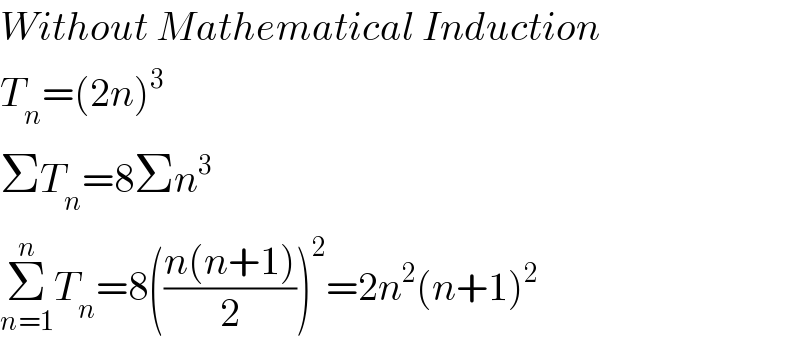
Without Mathematical Induction T_n =(2n)^3 ΣT_n =8Σn^3 Σ_(n=1) ^n T_n =8(((n(n+1))/2))^2 =2n^2 (n+1)^2
$${Without}\:{Mathematical}\:{Induction} \\ $$$${T}_{{n}} =\left(\mathrm{2}{n}\right)^{\mathrm{3}} \\ $$$$\Sigma{T}_{{n}} =\mathrm{8}\Sigma{n}^{\mathrm{3}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{n}} =\mathrm{8}\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$
Commented by JDamian last updated on 30/Jul/20
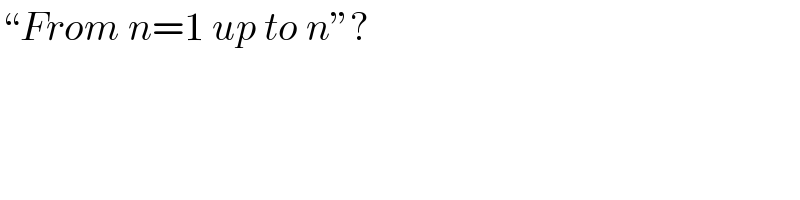
“From n=1 up to n”?
$$“{From}\:{n}=\mathrm{1}\:{up}\:{to}\:{n}''? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *