Menu Close

Prove-by-principle-of-mathematical-induction-sin-x-sin-2x-sin-3x-sin-nx-cos-1-2-x-cos-n-1-2-x-2-sin-1-2-x-

Tinku Tara 0 Comments
Pin




Question Number 60156 by Tawa1 last updated on 18/May/19
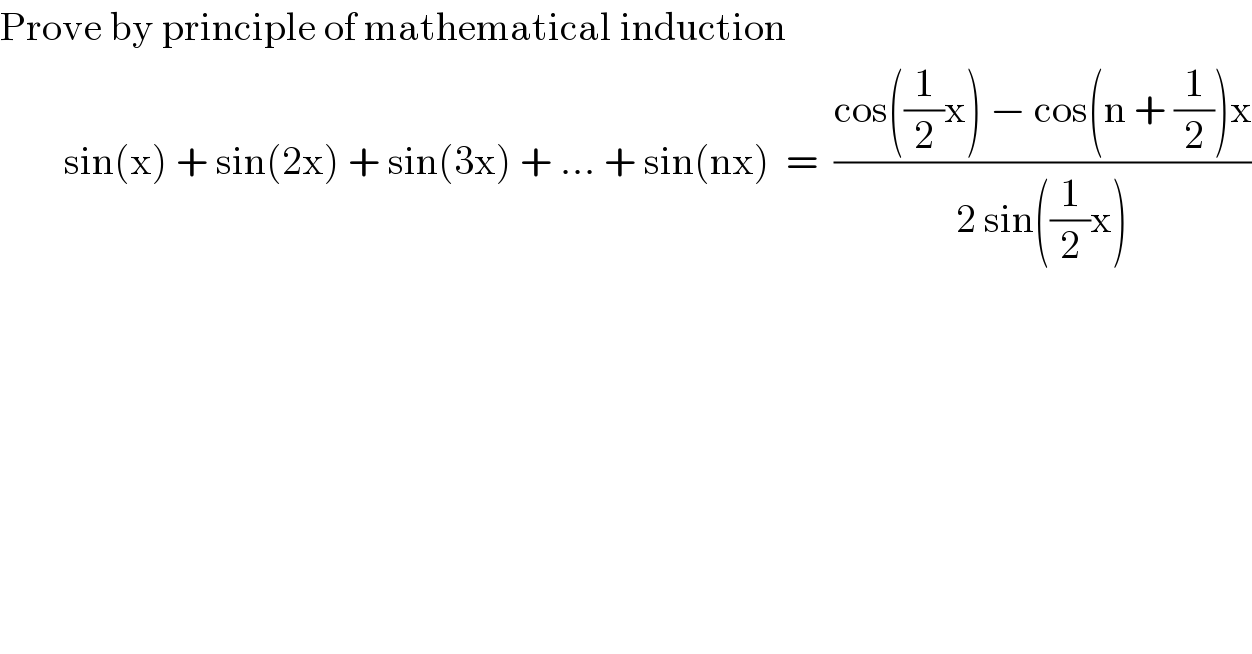
Prove by principle of mathematical induction sin(x) + sin(2x) + sin(3x) + ... + sin(nx) = ((cos((1/2)x) − cos(n + (1/2))x)/(2 sin((1/2)x)))
$$\mathrm{Prove}\:\mathrm{by}\:\mathrm{principle}\:\mathrm{of}\:\mathrm{mathematical}\:\mathrm{induction} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{x}\right)\:+\:\mathrm{sin}\left(\mathrm{2x}\right)\:+\:\mathrm{sin}\left(\mathrm{3x}\right)\:+\:…\:+\:\mathrm{sin}\left(\mathrm{nx}\right)\:\:=\:\:\frac{\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)\:−\:\mathrm{cos}\left(\mathrm{n}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}}{\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)} \\ $$
Commented by Smail last updated on 19/May/19
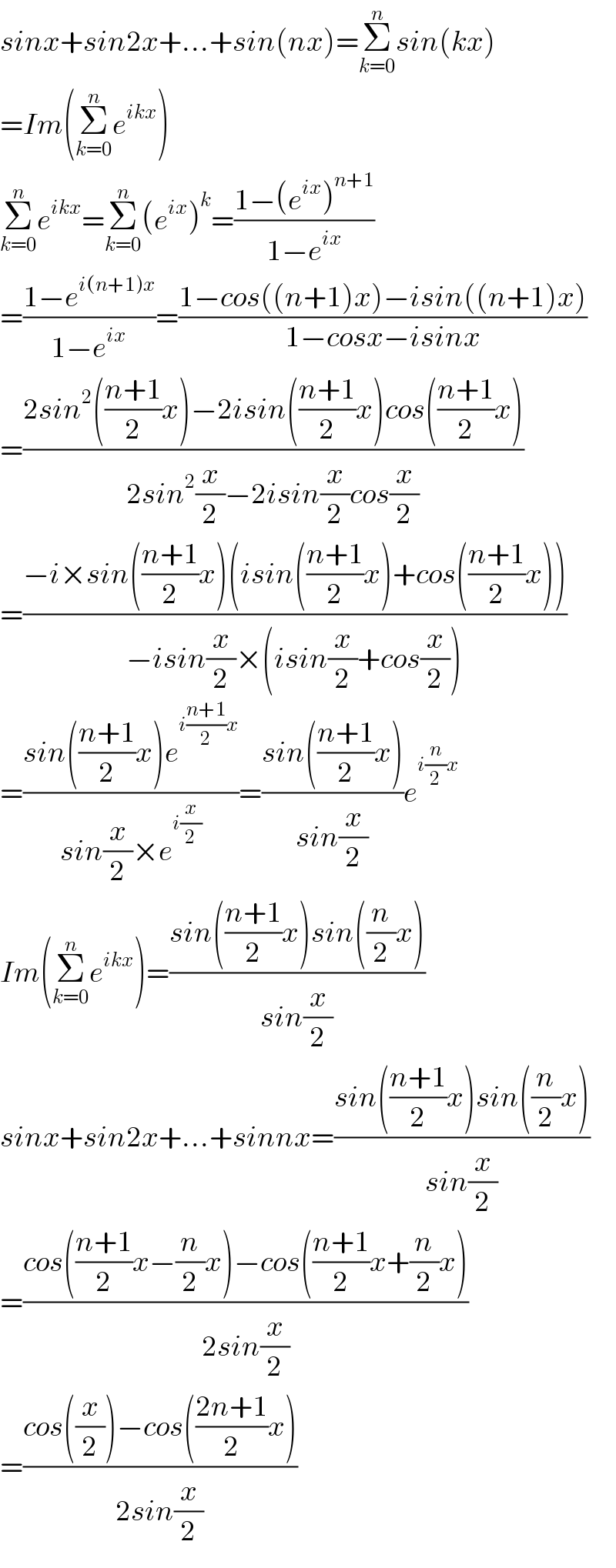
sinx+sin2x+...+sin(nx)=Σ_(k=0) ^n sin(kx) =Im(Σ_(k=0) ^n e^(ikx) ) Σ_(k=0) ^n e^(ikx) =Σ_(k=0) ^n (e^(ix) )^k =((1−(e^(ix) )^(n+1) )/(1−e^(ix) )) =((1−e^(i(n+1)x) )/(1−e^(ix) ))=((1−cos((n+1)x)−isin((n+1)x))/(1−cosx−isinx)) =((2sin^2 (((n+1)/2)x)−2isin(((n+1)/2)x)cos(((n+1)/2)x))/(2sin^2 (x/2)−2isin(x/2)cos(x/2))) =((−i×sin(((n+1)/2)x)(isin(((n+1)/2)x)+cos(((n+1)/2)x)))/(−isin(x/2)×(isin(x/2)+cos(x/2)))) =((sin(((n+1)/2)x)e^(i((n+1)/2)x) )/(sin(x/2)×e^(i(x/2)) ))=((sin(((n+1)/2)x))/(sin(x/2)))e^(i(n/2)x) Im(Σ_(k=0) ^n e^(ikx) )=((sin(((n+1)/2)x)sin((n/2)x))/(sin(x/2))) sinx+sin2x+...+sinnx=((sin(((n+1)/2)x)sin((n/2)x))/(sin(x/2))) =((cos(((n+1)/2)x−(n/2)x)−cos(((n+1)/2)x+(n/2)x))/(2sin(x/2))) =((cos((x/2))−cos(((2n+1)/2)x))/(2sin(x/2)))
$${sinx}+{sin}\mathrm{2}{x}+…+{sin}\left({nx}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{sin}\left({kx}\right) \\ $$$$={Im}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{ikx}} \right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{ikx}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({e}^{{ix}} \right)^{{k}} =\frac{\mathrm{1}−\left({e}^{{ix}} \right)^{{n}+\mathrm{1}} }{\mathrm{1}−{e}^{{ix}} } \\ $$$$=\frac{\mathrm{1}−{e}^{{i}\left({n}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{ix}} }=\frac{\mathrm{1}−{cos}\left(\left({n}+\mathrm{1}\right){x}\right)−{isin}\left(\left({n}+\mathrm{1}\right){x}\right)}{\mathrm{1}−{cosx}−{isinx}} \\ $$$$=\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)−\mathrm{2}{isin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right){cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{2}{isin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{−{i}×{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)\left({isin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)+{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)\right)}{−{isin}\frac{{x}}{\mathrm{2}}×\left({isin}\frac{{x}}{\mathrm{2}}+{cos}\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right){e}^{{i}\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}} }{{sin}\frac{{x}}{\mathrm{2}}×{e}^{{i}\frac{{x}}{\mathrm{2}}} }=\frac{{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{{sin}\frac{{x}}{\mathrm{2}}}{e}^{{i}\frac{{n}}{\mathrm{2}}{x}} \\ $$$${Im}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{{ikx}} \right)=\frac{{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right){sin}\left(\frac{{n}}{\mathrm{2}}{x}\right)}{{sin}\frac{{x}}{\mathrm{2}}} \\ $$$${sinx}+{sin}\mathrm{2}{x}+…+{sinnx}=\frac{{sin}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right){sin}\left(\frac{{n}}{\mathrm{2}}{x}\right)}{{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}−\frac{{n}}{\mathrm{2}}{x}\right)−{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}+\frac{{n}}{\mathrm{2}}{x}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{{cos}\left(\frac{{x}}{\mathrm{2}}\right)−{cos}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$
Commented by Tawa1 last updated on 19/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Kunal12588 last updated on 18/May/19
P(n): sin(x)+sin(2x)+sin(3x)+...+sin(nx)=((cos((1/2)x)−cos(n+(1/2))x)/(2 sin((1/2)x))) P(1) : LHS=sin(x) RHS=((cos((1/2)x)−cos(1 + (1/2))x)/(2 sin((1/2)x)))=((sin((((1/2)+1+(1/2))/2))x sin(((1+(1/2)−(1/2))/2))x)/(sin((1/2))x)) =((sin(x) sin((1/2))x)/(sin((1/2))x))=sin(x) ⇒LHS=RHS ∴P(1) is true Let P(k) be true ; k∈N P(k): sin(x)+sin(2x)+sin(3x)+...+sin(kx)=((cos((1/2))x−cos(k+ (1/2))x)/(2 sin((1/2))x)) Now, P(k+1): sin(x)+sin(2x)+...+sin(kx)+sin((k+1)x) =((cos((1/2))x−cos(k+ (1/2))x)/(2 sin((1/2))x))+sin((k+1)x) =((cos((1/2))x−cos(k+ (1/2))x)/(2 sin((1/2))x))+((2sin((k+1)x)sin((1/2))x)/(2sin((1/2))x)) =p+((cos((1/2)−k−1)x−cos((1/2)+k+1)x)/(2sin((1/2))x)) =p+((cos(k+(1/2))x−cos(k+1+(1/2))x)/(2sin((1/2))x)) =((cos((1/2))x−cos(k+(1/2))x+cos(k+(1/2))x−cos(k+1+(1/2))x)/(2sin((1/2))x)) =((cos((1/2))x−cos(k+1+(1/2))x)/(2sin((1/2))x)) ∴P(n) is true from Principle of Mathematical Induction
$${P}\left({n}\right):\:\mathrm{sin}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{3x}\right)+…+\mathrm{sin}\left(\mathrm{nx}\right)=\frac{\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)−\mathrm{cos}\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}}{\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)} \\ $$$${P}\left(\mathrm{1}\right)\::\: \\ $$$${LHS}={sin}\left({x}\right) \\ $$$${RHS}=\frac{\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)−\mathrm{cos}\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}}{\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}=\frac{{sin}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}\right){x}\:{sin}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}\right){x}}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$=\frac{{sin}\left({x}\right)\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}={sin}\left({x}\right) \\ $$$$\Rightarrow{LHS}={RHS} \\ $$$$\therefore{P}\left(\mathrm{1}\right)\:{is}\:{true} \\ $$$${Let}\:{P}\left({k}\right)\:\:{be}\:{true}\:;\:{k}\in\mathbb{N} \\ $$$${P}\left({k}\right):\:{sin}\left({x}\right)+{sin}\left(\mathrm{2}{x}\right)+{sin}\left(\mathrm{3}{x}\right)+…+{sin}\left({kx}\right)=\frac{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\:\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$${Now}, \\ $$$${P}\left({k}+\mathrm{1}\right): \\ $$$${sin}\left({x}\right)+{sin}\left(\mathrm{2}{x}\right)+…+{sin}\left({kx}\right)+{sin}\left(\left({k}+\mathrm{1}\right){x}\right) \\ $$$$=\frac{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\:\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}+{sin}\left(\left({k}+\mathrm{1}\right){x}\right) \\ $$$$=\frac{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\:\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}+\frac{\mathrm{2}{sin}\left(\left({k}+\mathrm{1}\right){x}\right){sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$={p}+\frac{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}−{k}−\mathrm{1}\right){x}−{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}+{k}+\mathrm{1}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$={p}+\frac{{cos}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$=\frac{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}+{cos}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$=\frac{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left({k}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$\therefore{P}\left({n}\right)\:{is}\:{true}\:{from}\:{Principle}\:{of}\:{Mathematical}\:{Induction} \\ $$
Commented by Tawa1 last updated on 18/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 18/May/19
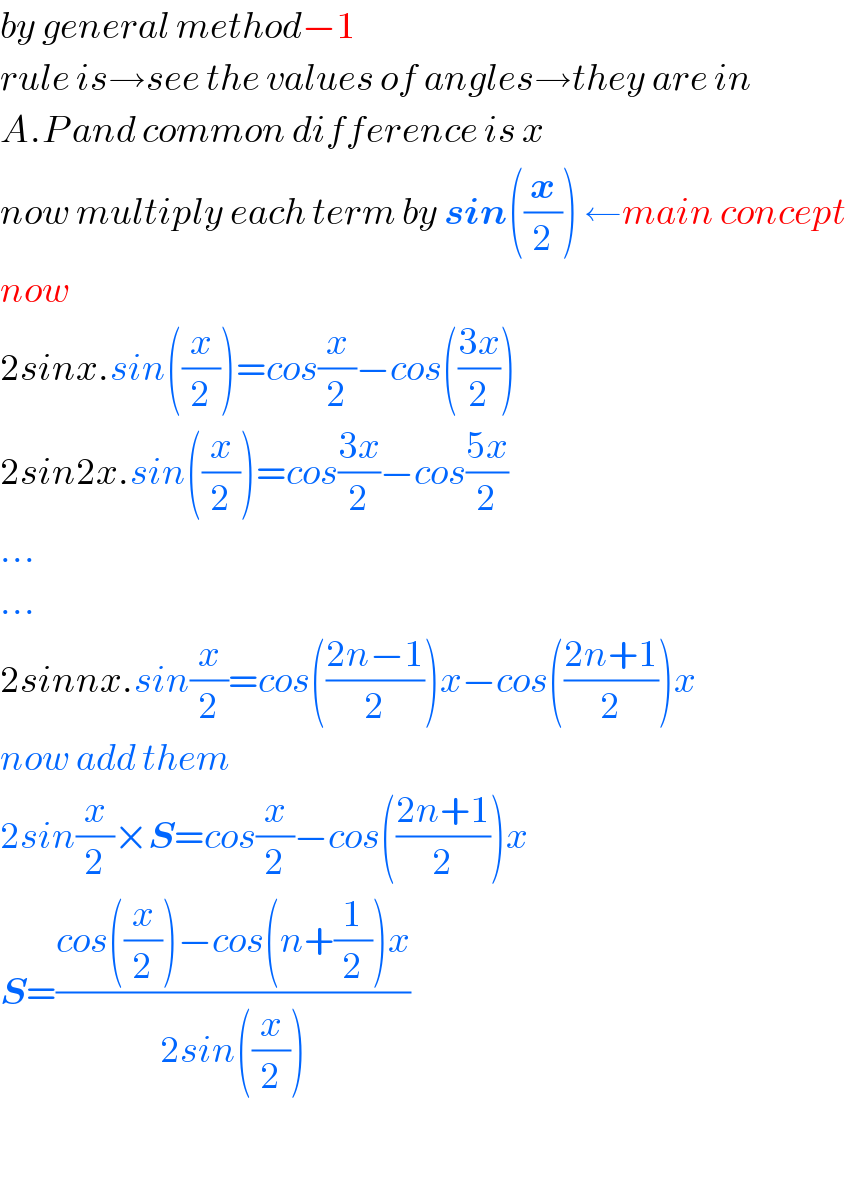
by general method−1 rule is→see the values of angles→they are in A.P and common difference is x now multiply each term by sin((x/2)) ←main concept now 2sinx.sin((x/2))=cos(x/2)−cos(((3x)/2)) 2sin2x.sin((x/2))=cos((3x)/2)−cos((5x)/2) ... ... 2sinnx.sin(x/2)=cos(((2n−1)/2))x−cos(((2n+1)/2))x now add them 2sin(x/2)×S=cos(x/2)−cos(((2n+1)/2))x S=((cos((x/2))−cos(n+(1/2))x)/(2sin((x/2))))
$${by}\:{general}\:{method}−\mathrm{1} \\ $$$${rule}\:{is}\rightarrow{see}\:{the}\:{values}\:{of}\:{angles}\rightarrow{they}\:{are}\:{in}\: \\ $$$${A}.{P}\:{and}\:{common}\:{difference}\:{is}\:{x} \\ $$$${now}\:{multiply}\:{each}\:{term}\:{by}\:\boldsymbol{{sin}}\left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\:\leftarrow{main}\:{concept} \\ $$$${now} \\ $$$$\mathrm{2}{sinx}.{sin}\left(\frac{{x}}{\mathrm{2}}\right)={cos}\frac{{x}}{\mathrm{2}}−{cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{sin}\mathrm{2}{x}.{sin}\left(\frac{{x}}{\mathrm{2}}\right)={cos}\frac{\mathrm{3}{x}}{\mathrm{2}}−{cos}\frac{\mathrm{5}{x}}{\mathrm{2}} \\ $$$$… \\ $$$$… \\ $$$$\mathrm{2}{sinnx}.{sin}\frac{{x}}{\mathrm{2}}={cos}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\right){x}−{cos}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right){x} \\ $$$${now}\:{add}\:{them} \\ $$$$\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}×\boldsymbol{{S}}={cos}\frac{{x}}{\mathrm{2}}−{cos}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right){x} \\ $$$$\boldsymbol{{S}}=\frac{{cos}\left(\frac{{x}}{\mathrm{2}}\right)−{cos}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$ \\ $$
Commented by Kunal12588 last updated on 18/May/19
that's actually great
Commented by Tawa1 last updated on 18/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 18/May/19
method−2 p=cosx+cos2x+cos3x+...+cosxnx q=sinx+sin2x+sin3x+...+sinnx p+iq=e^(ix) +e^(i2x) +...+e^(inx) p+iq=((e^(ix) (e^(inx) −1))/(e^(ix) −1)) p+iq=((e^(i(n+1)x) −e^(ix) )/(e^(ix) −1)) =((cos(n+1)x+isin(n+1)x−cosx−isinx)/(cosx+isinx−1)) =(([cos(n+1)x−cosx]+i[sin(n+1)x−sinx])/((cosx−1)+isinx)) =((2sin(x+((nx)/2))sin(((−nx)/2))+i[2cos(x+((nx)/2))sin(((nx)/2)))/(−2sin^2 (x/2)+i2sin(x/2)cos(x/2))) =((2sin((nx)/2))/(2sin(x/2)))×((−sin(x+((nx)/2))+icos(x+((nx)/2)))/(−sin(x/2)+icos(x/2))) =((sin((nx)/2))/(sin(x/2)))×(([sin(x+((nx)/2))−icos(x+((nx)/2))][sin(x/2)+icos(x/2)])/((sin(x/2)−icos(x/2))(sin(x/2)+icos(x/2)))) =((sin((nx)/2))/(sin(x/2)))×(([sin(x+((nx)/2))sin(x/2)+isin(x+((nx)/2))cos(x/2)−icos(x+((nx)/2))sin(x/2)+cos(x+((nx)/2))cos(x/2)])/(sin^2 (x/2)+cos^2 (x/2))) =((sin((nx)/2))/(sin(x/2)))×((cos(((nx)/2)+(x/2))+isin(((nx)/2)+(x/2)))/1) =[((sin((nx)/2))/(sin(x/2)))×cos(n+1)(x/2)]+i[((sin((nx)/2))/(sin(x/2)))×sin(n+1)(x/2)] =[((sin(((nx)/2)+((nx)/2)+(x/2))−sin((x/2)))/(2sin(x/2)))]+i[((cos(x/2)−cos(((nx)/2)+((nx)/2)+(x/2))/(2sin(x/2)))] So p=Σ_(r=1) ^n cosrx=[((sin(nx+(x/2)))/(2sin(x/2)))] q=Σ_(r=1) ^n sinrx=[((cos(x/2)−cos(nx+(x/2)))/(2sin(x/2)))] this is second method... =
$${method}−\mathrm{2} \\ $$$${p}={cosx}+{cos}\mathrm{2}{x}+{cos}\mathrm{3}{x}+…+{cosxnx} \\ $$$${q}={sinx}+{sin}\mathrm{2}{x}+{sin}\mathrm{3}{x}+…+{sinnx} \\ $$$${p}+{iq}={e}^{{ix}} +{e}^{{i}\mathrm{2}{x}} +…+{e}^{{inx}} \\ $$$${p}+{iq}=\frac{{e}^{{ix}} \left({e}^{{inx}} −\mathrm{1}\right)}{{e}^{{ix}} −\mathrm{1}} \\ $$$${p}+{iq}=\frac{{e}^{{i}\left({n}+\mathrm{1}\right){x}} −{e}^{{ix}} }{{e}^{{ix}} −\mathrm{1}} \\ $$$$=\frac{{cos}\left({n}+\mathrm{1}\right){x}+{isin}\left({n}+\mathrm{1}\right){x}−{cosx}−{isinx}}{{cosx}+{isinx}−\mathrm{1}} \\ $$$$=\frac{\left[{cos}\left({n}+\mathrm{1}\right){x}−{cosx}\right]+{i}\left[{sin}\left({n}+\mathrm{1}\right){x}−{sinx}\right]}{\left({cosx}−\mathrm{1}\right)+{isinx}} \\ $$$$=\frac{\mathrm{2}{sin}\left({x}+\frac{{nx}}{\mathrm{2}}\right){sin}\left(\frac{−{nx}}{\mathrm{2}}\right)+{i}\left[\mathrm{2}{cos}\left({x}+\frac{{nx}}{\mathrm{2}}\right){sin}\left(\frac{{nx}}{\mathrm{2}}\right)\right.}{−\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+{i}\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}{sin}\frac{{nx}}{\mathrm{2}}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}}×\frac{−{sin}\left({x}+\frac{{nx}}{\mathrm{2}}\right)+{icos}\left({x}+\frac{{nx}}{\mathrm{2}}\right)}{−{sin}\frac{{x}}{\mathrm{2}}+{icos}\frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{{sin}\frac{{nx}}{\mathrm{2}}}{{sin}\frac{{x}}{\mathrm{2}}}×\frac{\left[{sin}\left({x}+\frac{{nx}}{\mathrm{2}}\right)−{icos}\left({x}+\frac{{nx}}{\mathrm{2}}\right)\right]\left[{sin}\frac{{x}}{\mathrm{2}}+{icos}\frac{{x}}{\mathrm{2}}\right]}{\left({sin}\frac{{x}}{\mathrm{2}}−{icos}\frac{{x}}{\mathrm{2}}\right)\left({sin}\frac{{x}}{\mathrm{2}}+{icos}\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{{sin}\frac{{nx}}{\mathrm{2}}}{{sin}\frac{{x}}{\mathrm{2}}}×\frac{\left[{sin}\left({x}+\frac{{nx}}{\mathrm{2}}\right){sin}\frac{{x}}{\mathrm{2}}+{isin}\left({x}+\frac{{nx}}{\mathrm{2}}\right){cos}\frac{{x}}{\mathrm{2}}−{icos}\left({x}+\frac{{nx}}{\mathrm{2}}\right){sin}\frac{{x}}{\mathrm{2}}+{cos}\left({x}+\frac{{nx}}{\mathrm{2}}\right){cos}\frac{{x}}{\mathrm{2}}\right]}{{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$=\frac{{sin}\frac{{nx}}{\mathrm{2}}}{{sin}\frac{{x}}{\mathrm{2}}}×\frac{{cos}\left(\frac{{nx}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\right)+{isin}\left(\frac{{nx}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}} \\ $$$$=\left[\frac{{sin}\frac{{nx}}{\mathrm{2}}}{{sin}\frac{{x}}{\mathrm{2}}}×{cos}\left({n}+\mathrm{1}\right)\frac{{x}}{\mathrm{2}}\right]+{i}\left[\frac{{sin}\frac{{nx}}{\mathrm{2}}}{{sin}\frac{{x}}{\mathrm{2}}}×{sin}\left({n}+\mathrm{1}\right)\frac{{x}}{\mathrm{2}}\right] \\ $$$$=\left[\frac{{sin}\left(\frac{{nx}}{\mathrm{2}}+\frac{{nx}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\right)−{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}}\right]+{i}\left[\frac{{cos}\frac{{x}}{\mathrm{2}}−{cos}\left(\frac{{nx}}{\mathrm{2}}+\frac{{nx}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\right.}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}}\right] \\ $$$$\boldsymbol{{S}}{o} \\ $$$${p}=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{cosrx}=\left[\frac{{sin}\left({nx}+\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}}\right] \\ $$$${q}=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{sinrx}=\left[\frac{{cos}\frac{{x}}{\mathrm{2}}−{cos}\left({nx}+\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}}\right] \\ $$$${this}\:{is}\:{second}\:{method}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$= \\ $$
Commented by Tawa1 last updated on 18/May/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 18/May/19
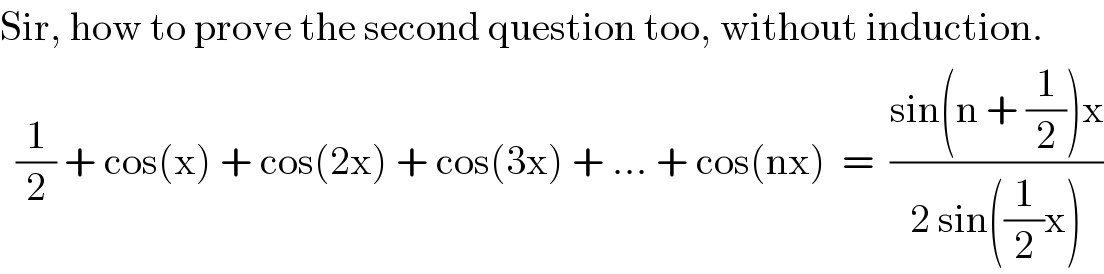
Sir, how to prove the second question too, without induction. (1/2) + cos(x) + cos(2x) + cos(3x) + ... + cos(nx) = ((sin(n + (1/2))x)/(2 sin((1/2)x)))
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{second}\:\mathrm{question}\:\mathrm{too},\:\mathrm{without}\:\mathrm{induction}. \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{cos}\left(\mathrm{x}\right)\:+\:\mathrm{cos}\left(\mathrm{2x}\right)\:+\:\mathrm{cos}\left(\mathrm{3x}\right)\:+\:…\:+\:\mathrm{cos}\left(\mathrm{nx}\right)\:\:=\:\:\frac{\mathrm{sin}\left(\mathrm{n}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}}{\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)} \\ $$
Commented by Tawa1 last updated on 18/May/19
Thanks for your time.
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by tanmay last updated on 18/May/19
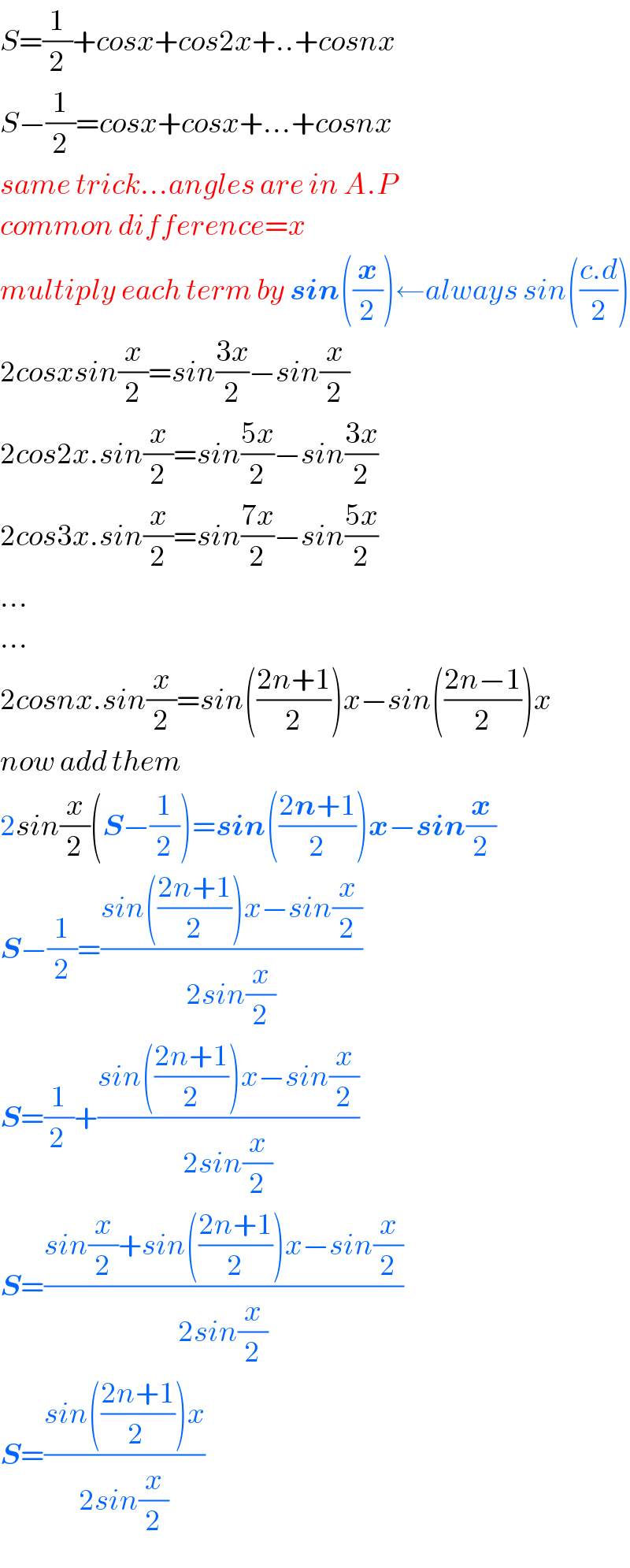
S=(1/2)+cosx+cos2x+..+cosnx S−(1/2)=cosx+cosx+...+cosnx same trick...angles are in A.P common difference=x multiply each term by sin((x/2))←always sin(((c.d)/2)) 2cosxsin(x/2)=sin((3x)/2)−sin(x/2) 2cos2x.sin(x/2)=sin((5x)/2)−sin((3x)/2) 2cos3x.sin(x/2)=sin((7x)/2)−sin((5x)/2) ... ... 2cosnx.sin(x/2)=sin(((2n+1)/2))x−sin(((2n−1)/2))x now add them 2sin(x/2)(S−(1/2))=sin(((2n+1)/2))x−sin(x/2) S−(1/2)=((sin(((2n+1)/2))x−sin(x/2))/(2sin(x/2))) S=(1/(2 ))+((sin(((2n+1)/2))x−sin(x/2))/(2sin(x/2))) S=((sin(x/2)+sin(((2n+1)/2))x−sin(x/2))/(2sin(x/2))) S=((sin(((2n+1)/(2 )))x)/(2sin(x/2)))
$${S}=\frac{\mathrm{1}}{\mathrm{2}}+{cosx}+{cos}\mathrm{2}{x}+..+{cosnx} \\ $$$${S}−\frac{\mathrm{1}}{\mathrm{2}}={cosx}+{cosx}+…+{cosnx} \\ $$$${same}\:{trick}…{angles}\:{are}\:{in}\:{A}.{P} \\ $$$${common}\:{difference}={x} \\ $$$${multiply}\:{each}\:{term}\:{by}\:\boldsymbol{{sin}}\left(\frac{\boldsymbol{{x}}}{\mathrm{2}}\right)\leftarrow{always}\:{sin}\left(\frac{{c}.{d}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{cosxsin}\frac{{x}}{\mathrm{2}}={sin}\frac{\mathrm{3}{x}}{\mathrm{2}}−{sin}\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{2}{cos}\mathrm{2}{x}.{sin}\frac{{x}}{\mathrm{2}}={sin}\frac{\mathrm{5}{x}}{\mathrm{2}}−{sin}\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$$$\mathrm{2}{cos}\mathrm{3}{x}.{sin}\frac{{x}}{\mathrm{2}}={sin}\frac{\mathrm{7}{x}}{\mathrm{2}}−{sin}\frac{\mathrm{5}{x}}{\mathrm{2}} \\ $$$$… \\ $$$$… \\ $$$$\mathrm{2}{cosnx}.{sin}\frac{{x}}{\mathrm{2}}={sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right){x}−{sin}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\right){x} \\ $$$${now}\:{add}\:{them} \\ $$$$\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}\left(\boldsymbol{{S}}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\boldsymbol{{sin}}\left(\frac{\mathrm{2}\boldsymbol{{n}}+\mathrm{1}}{\mathrm{2}}\right)\boldsymbol{{x}}−\boldsymbol{{sin}}\frac{\boldsymbol{{x}}}{\mathrm{2}} \\ $$$$\boldsymbol{{S}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{{sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right){x}−{sin}\frac{{x}}{\mathrm{2}}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$\boldsymbol{{S}}=\frac{\mathrm{1}}{\mathrm{2}\:}+\frac{{sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right){x}−{sin}\frac{{x}}{\mathrm{2}}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$\boldsymbol{{S}}=\frac{{sin}\frac{{x}}{\mathrm{2}}+{sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right){x}−{sin}\frac{{x}}{\mathrm{2}}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$$$\boldsymbol{{S}}=\frac{{sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}\:}\right){x}}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$
Commented by Tawa1 last updated on 18/May/19
I really appreciate sir. God bless you.
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by malwaan last updated on 19/May/19
FANTASTIC sir
$$\mathcal{FANTASTIC}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *