Question Number 173820 by dragan91 last updated on 18/Jul/22
$$ \\ $$ Prove
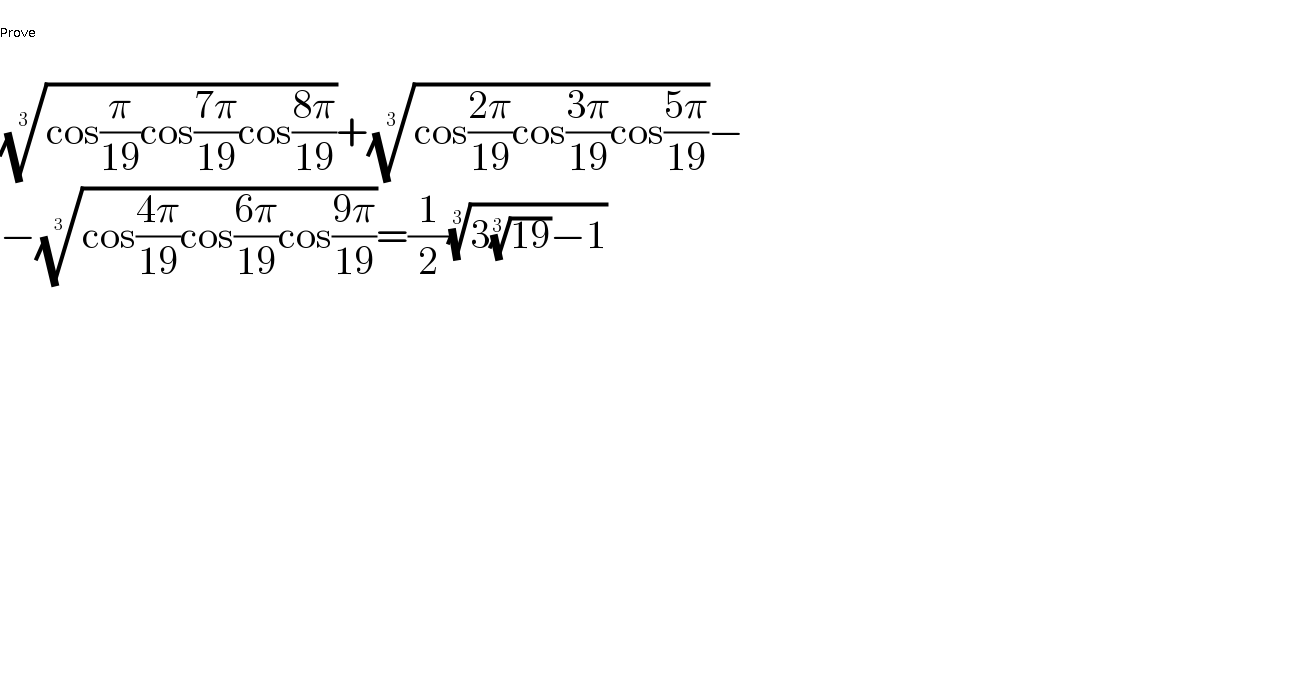
$$ \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{cos}\frac{\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{7}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{8}\pi}{\mathrm{19}}}+\sqrt[{\mathrm{3}}]{\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{5}\pi}{\mathrm{19}}}− \\ $$$$−\sqrt[{\mathrm{3}}]{\mathrm{cos}\frac{\mathrm{4}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{6}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{9}\pi}{\mathrm{19}}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{19}}−\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
$$ \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{cos}\frac{\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{7}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{8}\pi}{\mathrm{19}}}+\sqrt[{\mathrm{3}}]{\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{3}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{5}\pi}{\mathrm{19}}}− \\ $$$$−\sqrt[{\mathrm{3}}]{\mathrm{cos}\frac{\mathrm{4}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{6}\pi}{\mathrm{19}}\mathrm{cos}\frac{\mathrm{9}\pi}{\mathrm{19}}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{19}}−\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
