Question Number 98270 by M±th+et+s last updated on 12/Jun/20
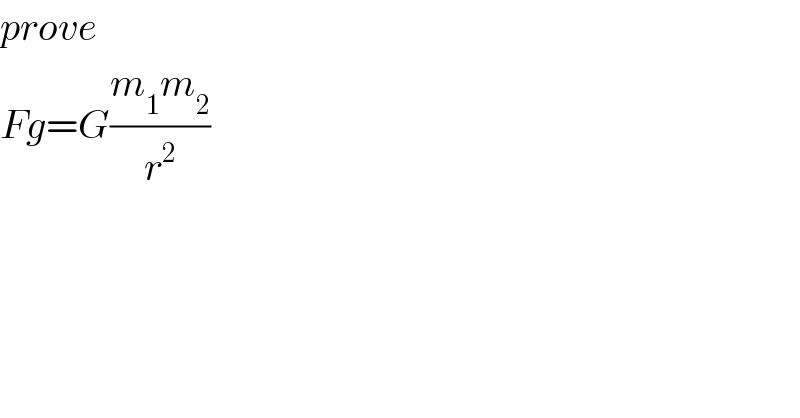
$${prove} \\ $$$${Fg}={G}\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} }{{r}^{\mathrm{2}} } \\ $$
Answered by Rio Michael last updated on 12/Jun/20

$$\mathrm{Newton}:\mathrm{s}\:\mathrm{law}\:\mathrm{of}\:\mathrm{universal}\:\mathrm{gravitation}\:\mathrm{states}\:\mathrm{that}:\:''\:\mathrm{the}\:\mathrm{force} \\ $$$$\mathrm{between}\:\mathrm{two}\:\mathrm{point}\:\mathrm{mass}\:{m}_{\mathrm{1}} \:\mathrm{and}\:\:{m}_{\mathrm{2}} \:\mathrm{seperated}\:\mathrm{by}\:\mathrm{a}\:\mathrm{distance}\:{r} \\ $$$$\mathrm{is}\:\mathrm{directly}\:\mathrm{proportional}\:\mathrm{to}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{thier}\:\mathrm{masses}\:\mathrm{and}\:\mathrm{inversly} \\ $$$$\mathrm{proportional}\:\mathrm{to}\:\mathrm{the}\:\mathrm{square}\:\mathrm{of}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{seperating}\:\mathrm{them}'' \\ $$$$\mathrm{thus}\:{F}\:\propto\:{m}_{\mathrm{1}} {m}_{\mathrm{2}} \:…..\left({i}\right) \\ $$$${F}\:\propto\:\frac{\mathrm{1}}{{r}^{\mathrm{2}} \:}\:……\left({ii}\right) \\ $$$$\Rightarrow\:{F}\:\propto\:\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} }{{r}^{\mathrm{2}} }\:\Rightarrow\:{F}\:=\:{k}\:\frac{{m}_{\mathrm{1}} \:{m}_{\mathrm{2}} }{{r}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{k}\:=\:\frac{{Fr}^{\mathrm{2}} }{{m}_{\mathrm{1}} {m}_{\mathrm{2}} \:}\:\mathrm{according}\:\mathrm{to}\:\mathrm{the}\:\mathrm{cavendish}\:\mathrm{experiment}, \\ $$$$\mathrm{this}\:\mathrm{ratio}\:=\:\mathrm{6}.\mathrm{67}\:×\:\mathrm{10}^{−\mathrm{11}} \:\mathrm{N}\:\mathrm{m}^{\mathrm{2}} \:\mathrm{kg}^{−\mathrm{2}} \: \\ $$$$\mathrm{in}\:\mathrm{physics}\:\mathrm{this}\:\mathrm{constant}\:=\:{G}\: \\ $$$$\Rightarrow\:{k}\:=\:{G} \\ $$$$\mathrm{thus}\:\:{F}\:=\:{G}\:\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} }{{r}^{\mathrm{2}} }\: \\ $$
Commented by M±th+et+s last updated on 12/Jun/20

$${thank}\:{you}\:{sir} \\ $$
Answered by smridha last updated on 13/Jun/20

$$\boldsymbol{{this}}\:{is}\:\boldsymbol{{very}}\:\boldsymbol{{silly}}\:\boldsymbol{{question}}!!\boldsymbol{{don}}'\boldsymbol{{t}} \\ $$$$\boldsymbol{{mind}}..\boldsymbol{{but}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}.\boldsymbol{{we}}\:\boldsymbol{{derived}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{formula}}\:\boldsymbol{{from}}\:\boldsymbol{{N}}{ew}\boldsymbol{{ton}}'{s} \\ $$$$\boldsymbol{{gravitational}}\:\boldsymbol{{law}}…\boldsymbol{{which}}\:\boldsymbol{{is}}\:\boldsymbol{{a}} \\ $$$$\boldsymbol{{statement}}\:\boldsymbol{{whoes}}\:\boldsymbol{{mathematical}} \\ $$$$\boldsymbol{{expression}}\:\boldsymbol{{is}}\:\boldsymbol{{that}}…\boldsymbol{{you}}\:\boldsymbol{{cannot}} \\ $$$$\boldsymbol{{prove}}\:\boldsymbol{{any}}\:\boldsymbol{{postulate}}!! \\ $$$$\boldsymbol{{but}}\:\boldsymbol{{it}}'{s}\:\boldsymbol{{true}}\:\boldsymbol{{that}}\:\boldsymbol{{it}}\:\boldsymbol{{can}}\:\boldsymbol{{be}}\:\boldsymbol{{shown}} \\ $$$$\boldsymbol{{from}}\:\boldsymbol{{E}}{i}\boldsymbol{{nstein}}\:\boldsymbol{{G}}{e}\boldsymbol{{neral}}\:\boldsymbol{{relativity}} \\ $$$$\boldsymbol{{with}}\:\boldsymbol{{much}}\:\boldsymbol{{more}}\:\boldsymbol{{approximation}}. \\ $$$$\boldsymbol{{And}}\:\boldsymbol{{once}}\:\boldsymbol{{more}}\:\boldsymbol{{fact}}\:\boldsymbol{{I}}\:\boldsymbol{{want}}\:\boldsymbol{{to}} \\ $$$$\boldsymbol{{share}}\:\boldsymbol{{that}}\:\boldsymbol{{dont}}\:\boldsymbol{{call}}\:\boldsymbol{{Newton}}'\boldsymbol{{s}} \\ $$$$\:{gra}\boldsymbol{{vitational}}\:\boldsymbol{{L}}{aw}\:\boldsymbol{{is}}\:\boldsymbol{{universal}} \\ $$$$\boldsymbol{{law}}…\boldsymbol{{because}}\:\boldsymbol{{it}}\:\boldsymbol{{does}}\:\boldsymbol{{not}}\:\boldsymbol{{vallid}} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{strong}}\:\boldsymbol{{gravitational}}\:\boldsymbol{{field}}, \\ $$$$\boldsymbol{{but}}\:\boldsymbol{{E}}{in}\boldsymbol{{stein}}'\:\boldsymbol{{G}}{T}\boldsymbol{{R}}\:\boldsymbol{{can}}\:\:\boldsymbol{{explain}}\: \\ $$$$\boldsymbol{{how}}\:\boldsymbol{{gravity}}\:\boldsymbol{{works}}…\boldsymbol{{this}}\:\boldsymbol{{the}} \\ $$$$\boldsymbol{{regorus}}\:\boldsymbol{{description}}\:\boldsymbol{{about}} \\ $$$$\boldsymbol{{gravity}}….. \\ $$$$\:\:\:\:\boldsymbol{{G}}_{\boldsymbol{\mu\nu}} =\:\boldsymbol{{R}}_{\boldsymbol{\mu}\nu} −\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{Rg}}_{\boldsymbol{\mu\nu}} =\frac{\mathrm{8}\boldsymbol{\pi{G}}}{\boldsymbol{{c}}^{\mathrm{4}} }\boldsymbol{{T}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{called}}\:\boldsymbol{{the}}\:\boldsymbol{{Einstein}}'\boldsymbol{{s}}\: \\ $$$$\boldsymbol{{tensor}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} .\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{explanation}} \\ $$$$\boldsymbol{{of}}\:\boldsymbol{{how}}\:\boldsymbol{{gravity}}\:\boldsymbol{{works}}…\boldsymbol{{what}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{gravity}}??? \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 13/Jun/20
$${nice}\:{explaining}\:{sir} \\ $$
