Question Number 88547 by ajfour last updated on 11/Apr/20
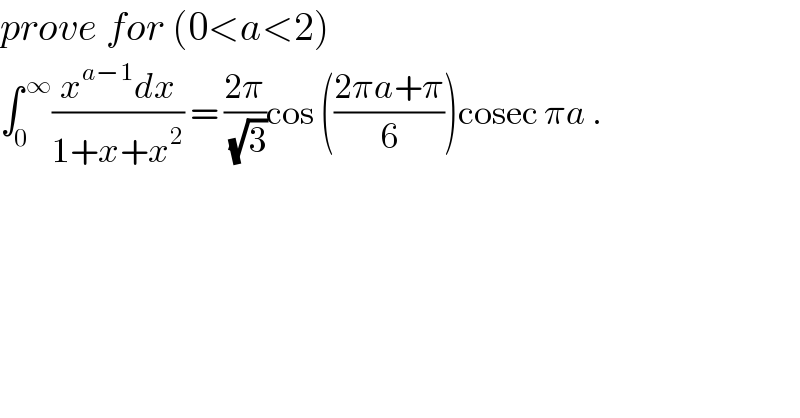
$${prove}\:{for}\:\left(\mathrm{0}<{a}<\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\:\left(\frac{\mathrm{2}\pi{a}+\pi}{\mathrm{6}}\right)\mathrm{cosec}\:\pi{a}\:. \\ $$
Answered by mind is power last updated on 12/Apr/20

$$\int_{−\infty} ^{+\infty} \frac{{x}^{{a}−\mathrm{1}} }{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }+\int_{\mathrm{0}} ^{+\infty} \frac{\left(−\mathrm{1}\right)^{{a}−\mathrm{1}} {x}^{{a}−\mathrm{1}} }{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{{C}_{{R}} } \frac{{x}^{{a}−\mathrm{1}} }{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\leqslant\int_{\mathrm{0}} ^{\pi} \frac{{R}^{{a}} {e}^{{i}\left({a}−\mathrm{1}\right)\pi} }{{R}^{\mathrm{2}} −{R}+\mathrm{1}}\rightarrow\mathrm{0} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{{i}\pi\left({a}−\mathrm{1}\right)} {x}^{{a}−\mathrm{1}} }{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}+\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}=\mathrm{2}{i}\pi{Res}\left(\frac{{z}^{{a}−\mathrm{1}} }{{z}^{\mathrm{2}} +{z}+\mathrm{1}},{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right) \\ $$$$=\frac{\mathrm{2}{i}\pi{e}^{{i}\left({a}−\mathrm{1}\right)\frac{\mathrm{2}\pi}{\mathrm{3}}} }{\left(\mathrm{3}{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} +\mathrm{1}\right)}=−{isin}\left(\pi{a}\right)\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+−{cos}\left(\pi{a}\right)\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$+\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$\frac{\mathrm{2}{i}\pi{e}^{{i}\left({a}−\mathrm{1}\right)\frac{\mathrm{2}\pi}{\mathrm{3}}} }{\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\mathrm{1}}=\frac{\mathrm{2}{i}\pi{e}^{{i}\left({a}−\mathrm{1}\right)\frac{\mathrm{2}\pi}{\mathrm{3}}} }{{i}\sqrt{\mathrm{3}}}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\left({cos}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right)+{isin}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right)\right) \\ $$$$=−{isin}\left(\pi{a}\right)\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−{cos}\left(\pi{a}\right)\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{2}{i}\pi}{\:\sqrt{\mathrm{3}}}{sin}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right)=−{isin}\left(\pi{a}\right)\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}=\frac{−\mathrm{2}\pi{sin}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right)}{{sin}\left(\pi{a}\right)\sqrt{\mathrm{3}}}\: \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{{a}−\mathrm{1}} {dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}{cos}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right)+\frac{−\mathrm{2}\pi{sin}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right){cos}\left(\pi{a}\right)}{{sin}\left(\pi{a}\right)\sqrt{\mathrm{3}}} \\ $$$$=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}.\frac{\mathrm{1}}{{sin}\left(\pi{a}\right)}\left\{{cos}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right){sin}\left(\pi{a}\right)−{sin}\left(\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right){cos}\left(\pi{a}\right)\right) \\ $$$$=\frac{\mathrm{2}\pi}{{sin}\left(\pi{a}\right)\sqrt{\mathrm{3}}}\left\{{sin}\left(\pi{a}−\frac{\mathrm{2}\pi\left({a}−\mathrm{1}\right)}{\mathrm{3}}\right)\right\} \\ $$$$=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}{sin}\left(\pi{a}\right)}\left\{{sin}\left(\frac{\pi{a}}{\mathrm{3}}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right\} \\ $$$$=\frac{\mathrm{2}\pi}{{sin}\left(\pi{a}\right)\sqrt{\mathrm{3}}}{cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi{a}}{\mathrm{3}}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=\frac{\mathrm{2}\pi}{{sin}\left(\pi{a}\right)\sqrt{\mathrm{3}}}\left({cos}\left(\frac{−\pi{a}}{\mathrm{3}}−\frac{\pi}{\mathrm{6}}\right)\right) \\ $$$$=\frac{\mathrm{2}\pi}{{sin}\left(\pi{a}\right)\sqrt{\mathrm{3}}}{cos}\left(\frac{\mathrm{2}\pi{a}+\pi}{\mathrm{6}}\right)=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}{cos}\left(\frac{\mathrm{2}\pi{a}+\pi}{\mathrm{6}}\right){cosec}\left(\pi{a}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 12/Apr/20
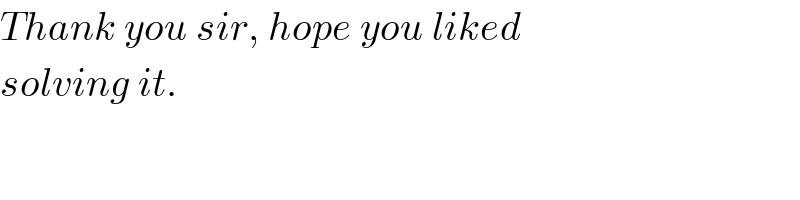
$${Thank}\:{you}\:{sir},\:{hope}\:{you}\:{liked} \\ $$$${solving}\:{it}. \\ $$
Commented by mind is power last updated on 12/Apr/20

$${nice}\:{one}\:{Sir} \\ $$$${since}\:\mathrm{4}\:{or}\:\mathrm{5}\:{month}\:{ago}\:{i}\:{lost}\:{my}\:{motivation} \\ $$$${lost}\:{pleasur}\:{of}\:{solving}\:{problemes}\:{i}\:{dont}\:{know}\:{why}! \\ $$$$ \\ $$
