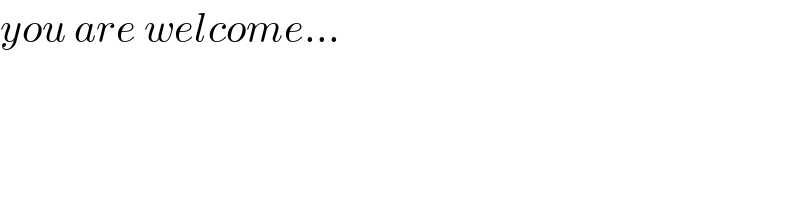Menu Close

Prove-it-sin-pi-2m-1-sin-2pi-2m-1-sin-mpi-2m-1-2m-1-2-m-

Tinku Tara 0 Comments
Pin




Question Number 127206 by MathSh last updated on 27/Dec/20
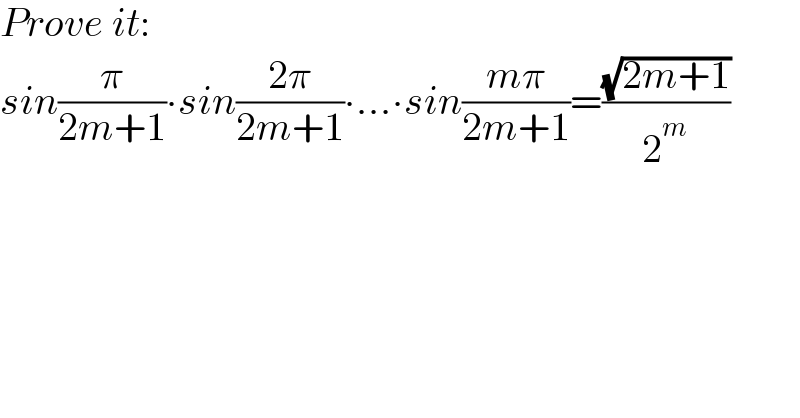
Prove it: sin(π/(2m+1))∙sin((2π)/(2m+1))∙...∙sin((mπ)/(2m+1))=((√(2m+1))/2^m )
$${Prove}\:{it}: \\ $$$${sin}\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\centerdot{sin}\frac{\mathrm{2}\pi}{\mathrm{2}{m}+\mathrm{1}}\centerdot…\centerdot{sin}\frac{{m}\pi}{\mathrm{2}{m}+\mathrm{1}}=\frac{\sqrt{\mathrm{2}{m}+\mathrm{1}}}{\mathrm{2}^{{m}} } \\ $$
Answered by Olaf last updated on 28/Dec/20
Ω = Π_(k=1) ^(k=m) sin(((kπ)/(2m+1))) Solve (z+1)^(2m+1) = 1 (1) z_k = e^((2ikπ)/(2m+1)) −1, k = 0,1,2,...,2m z_k = 2ie^((ikπ)/(2m+1)) sin(((kπ)/(2m+1))) Let P(z) = Σ_(k=0) ^(2m) (z+1)^k (2) ⇒ P(0) = 2m+1 (3) P(z) = 0 ⇔ Σ_(k=0) ^(2m) (z+1)^k = 0 ⇔ (((z+1)^(2m+1) −1)/((z+1)−1)) = 0, z≠0 ⇔ z = z_k , k = 1,2,...,2m (4) (2) and (4) : P(z) = Π_(k=1) ^(2m) (z−z_k ) ⇒ P(0) = Π_(k=1) ^(2m) (−z_k ) = Π_(k=1) ^(2m) z_k P(0) = Π_(k=1) ^(2m) [2ie^((ikπ)/(2m+1)) sin(((kπ)/(2m+1)))] P(0) = 2^(2m) i^(2m) e^(((2m(2m+1))/2).((iπ)/(2m+1))) Π_(k=1) ^(2m) sin(((kπ)/(2m+1))) P(0) = 2^(2m) (−1)^m e^(imπ) Π_(k=1) ^(2m) sin(((kπ)/(2m+1))) P(0) = 2^(2m) Π_(k=1) ^(2m) sin(((kπ)/(2m+1))) (5) (3) and (5) : P(0) = 2m+1 = 2^(2m) Π_(k=1) ^(2m) sin(((kπ)/(2m+1))) ⇒ Π_(k=1) ^(2m) sin(((kπ)/(2m+1))) = ((2m+1)/2^(2m) ) (6) But sin(((kπ)/(2m+1))) = sin(π−((kπ)/(2m+1))) = sin((((2m+1−k)π)/(2m+1))) For example : sin((π/(2m+1))) = sin(((2mπ)/(2m+1))) ⇒ Π_(k=1) ^(2m) sin(((kπ)/(2m+1))) = Π_(k=1) ^m sin^2 (((kπ)/(2m+1))) = (Π_(k=1) ^m sin(((kπ)/(2m+1))))^2 = Ω^2 (7) (6) and (7) : Ω = ((√(2m+1))/2^m )
$$ \\ $$$$\Omega\:=\:\underset{{k}=\mathrm{1}} {\overset{{k}={m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\mathrm{Solve}\:\left({z}+\mathrm{1}\right)^{\mathrm{2}{m}+\mathrm{1}} \:=\:\mathrm{1}\:\left(\mathrm{1}\right) \\ $$$${z}_{{k}} \:=\:{e}^{\frac{\mathrm{2}{ik}\pi}{\mathrm{2}{m}+\mathrm{1}}} −\mathrm{1},\:{k}\:=\:\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{2}{m} \\ $$$${z}_{{k}} \:=\:\mathrm{2}{ie}^{\frac{{ik}\pi}{\mathrm{2}{m}+\mathrm{1}}} \mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\mathrm{Let}\:\mathrm{P}\left({z}\right)\:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{m}} {\sum}}\left({z}+\mathrm{1}\right)^{{k}} \:\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:\mathrm{P}\left(\mathrm{0}\right)\:=\:\mathrm{2}{m}+\mathrm{1}\:\left(\mathrm{3}\right) \\ $$$$\mathrm{P}\left({z}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{m}} {\sum}}\left({z}+\mathrm{1}\right)^{{k}} \:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\frac{\left({z}+\mathrm{1}\right)^{\mathrm{2}{m}+\mathrm{1}} −\mathrm{1}}{\left({z}+\mathrm{1}\right)−\mathrm{1}}\:=\:\mathrm{0},\:{z}\neq\mathrm{0} \\ $$$$\Leftrightarrow\:{z}\:=\:{z}_{{k}} ,\:{k}\:=\:\mathrm{1},\mathrm{2},…,\mathrm{2}{m}\:\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{4}\right)\:: \\ $$$$\mathrm{P}\left({z}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\left({z}−{z}_{{k}} \right) \\ $$$$\Rightarrow\:\mathrm{P}\left(\mathrm{0}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\left(−{z}_{{k}} \right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}{z}_{{k}} \\ $$$$\mathrm{P}\left(\mathrm{0}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\left[\mathrm{2}{ie}^{\frac{{ik}\pi}{\mathrm{2}{m}+\mathrm{1}}} \mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\right] \\ $$$$\mathrm{P}\left(\mathrm{0}\right)\:=\:\mathrm{2}^{\mathrm{2}{m}} {i}^{\mathrm{2}{m}} {e}^{\frac{\mathrm{2}{m}\left(\mathrm{2}{m}+\mathrm{1}\right)}{\mathrm{2}}.\frac{{i}\pi}{\mathrm{2}{m}+\mathrm{1}}} \underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\mathrm{P}\left(\mathrm{0}\right)\:=\:\mathrm{2}^{\mathrm{2}{m}} \left(−\mathrm{1}\right)^{{m}} {e}^{{im}\pi} \underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\mathrm{P}\left(\mathrm{0}\right)\:=\:\mathrm{2}^{\mathrm{2}{m}} \underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\:\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{5}\right)\:: \\ $$$$\mathrm{P}\left(\mathrm{0}\right)\:=\:\mathrm{2}{m}+\mathrm{1}\:=\:\mathrm{2}^{\mathrm{2}{m}} \underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\:=\:\frac{\mathrm{2}{m}+\mathrm{1}}{\mathrm{2}^{\mathrm{2}{m}} }\:\left(\mathrm{6}\right) \\ $$$$\mathrm{But}\:\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\:=\:\mathrm{sin}\left(\pi−\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$=\:\mathrm{sin}\left(\frac{\left(\mathrm{2}{m}+\mathrm{1}−{k}\right)\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\mathrm{For}\:\mathrm{example}\:: \\ $$$$\mathrm{sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\:=\:\mathrm{sin}\left(\frac{\mathrm{2}{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\mathrm{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$=\:\left(\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\right)^{\mathrm{2}} \:=\:\Omega^{\mathrm{2}} \:\left(\mathrm{7}\right) \\ $$$$\left(\mathrm{6}\right)\:\mathrm{and}\:\left(\mathrm{7}\right)\::\:\Omega\:=\:\frac{\sqrt{\mathrm{2}{m}+\mathrm{1}}}{\mathrm{2}^{{m}} } \\ $$
Commented by MathSh last updated on 28/Dec/20
Thanks sir
$${Thanks}\:{sir} \\ $$
Answered by mnjuly1970 last updated on 28/Dec/20
z^(2m+1) −1=0 , z∈C(roots::=1,z_1 ,...,z_(2m) ) z=re^(iθ) r^(2m+1) e^(i(2m+1)θ) =1=1.e^(i2kπ) θ_k =((2kπ)/(2m+1)) ⇒z_k =e^((i(2kπ))/(2m+1)) (k∈{0,1,2,...,2m}) (z−1)(z^(2m) +z^(2m−1) +...+z+1)=0 P(z)=z^(2m) +z^(2m−1) +...+z+1 P(z)=(z−z_1 )(z−z_2 )...(z−z_(2m) ) P(1)=(1−z_1 )(1−z_2 )...(1−z_(2m) )=2m+1 ∣1−z_1 ∣∣z−z_2 ∣....∣z−z_(2m) ∣=2m+1 ∣1−e^((i2π)/(2m+1)) ∣∣1−e^((i4π)/(2m+1)) ∣...∣1−e^((i(2(2mπ)))/(2m+1)) ∣=2m+1 2^(2m) sin((π/(2m+1)))sin(((2π)/(2m+1)))...sin(((mπ)/(2m+1)))sin((((m+1)π)/(2m+1)))...sin(((2mπ)/(2m+1)))=2m+1(∗) note:∣sin(θ)−icos(θ)∣=1 note:1−cos(2θ)=2sin^2 (θ) note: sin(2θ)=2sin(θ)cos(θ) note:sin(((2mπ)/(2m+1)))=sin(π−((2mπ)/(2m+1)))=sin((π/(2m+1))) ⋮ sin((((m+1)π)/(2m+1)))=sin(π−(((m+1)π)/(2m+1)))=sin(((mπ)/(2m+1))) example:∣1−e^((i2π)/(2m+1)) ∣=∣1−cos(((2π)/(2m+1)))−isin(((2π)/(2m+1)))∣ =∣2sin^2 ((π/(2m+1)))−2isin((π/(2m+1)))cos((π/(2m+1)))∣ =2sin((π/(2m+1)))∣sin((π/(2m+1)))−icos((π/(2m+1)))∣=2sin((π/(2m+1))) from (∗) and( notes)=:: 2^(2m) (sin((π/(2m+1)))...sin(((mπ)/(2m+1))))^2 =2m+1 sin((π/(2m+1)))...sin(((mπ)/(2m+1)))=((√(2m+1))/2^m ) ✓
$${z}^{\mathrm{2}{m}+\mathrm{1}} −\mathrm{1}=\mathrm{0}\:\:,\:{z}\in\mathbb{C}\left({roots}::=\mathrm{1},{z}_{\mathrm{1}} ,…,{z}_{\mathrm{2}{m}} \right) \\ $$$$\:{z}={re}^{{i}\theta} \\ $$$$\:{r}^{\mathrm{2}{m}+\mathrm{1}} {e}^{{i}\left(\mathrm{2}{m}+\mathrm{1}\right)\theta} =\mathrm{1}=\mathrm{1}.{e}^{{i}\mathrm{2}{k}\pi} \: \\ $$$$\theta_{{k}} =\frac{\mathrm{2}{k}\pi}{\mathrm{2}{m}+\mathrm{1}}\:\Rightarrow{z}_{{k}} ={e}^{\frac{{i}\left(\mathrm{2}{k}\pi\right)}{\mathrm{2}{m}+\mathrm{1}}} \:\left({k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{2}{m}\right\}\right) \\ $$$$\:\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{m}} +{z}^{\mathrm{2}{m}−\mathrm{1}} +…+{z}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:{P}\left({z}\right)={z}^{\mathrm{2}{m}} +{z}^{\mathrm{2}{m}−\mathrm{1}} +…+{z}+\mathrm{1} \\ $$$$\:\:\:{P}\left({z}\right)=\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)…\left({z}−{z}_{\mathrm{2}{m}} \right) \\ $$$$\:\:\:\:{P}\left(\mathrm{1}\right)=\left(\mathrm{1}−{z}_{\mathrm{1}} \right)\left(\mathrm{1}−{z}_{\mathrm{2}} \right)…\left(\mathrm{1}−{z}_{\mathrm{2}{m}} \right)=\mathrm{2}{m}+\mathrm{1} \\ $$$$\:\:\:\mid\mathrm{1}−{z}_{\mathrm{1}} \mid\mid{z}−{z}_{\mathrm{2}} \mid….\mid{z}−{z}_{\mathrm{2}{m}} \mid=\mathrm{2}{m}+\mathrm{1} \\ $$$$\:\:\:\mid\mathrm{1}−{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{2}{m}+\mathrm{1}}} \mid\mid\mathrm{1}−{e}^{\frac{{i}\mathrm{4}\pi}{\mathrm{2}{m}+\mathrm{1}}} \mid…\mid\mathrm{1}−{e}^{\frac{{i}\left(\mathrm{2}\left(\mathrm{2}{m}\pi\right)\right)}{\mathrm{2}{m}+\mathrm{1}}} \mid=\mathrm{2}{m}+\mathrm{1} \\ $$$$\:\:\mathrm{2}^{\mathrm{2}{m}} {sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right){sin}\left(\frac{\mathrm{2}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)…{sin}\left(\frac{{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right){sin}\left(\frac{\left({m}+\mathrm{1}\right)\pi}{\mathrm{2}{m}+\mathrm{1}}\right)…{sin}\left(\frac{\mathrm{2}{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)=\mathrm{2}{m}+\mathrm{1}\left(\ast\right) \\ $$$${note}:\mid{sin}\left(\theta\right)−{icos}\left(\theta\right)\mid=\mathrm{1} \\ $$$$\:\:{note}:\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)=\mathrm{2}{sin}^{\mathrm{2}} \left(\theta\right) \\ $$$$\:\:\:\:\:\:\:\:{note}:\:{sin}\left(\mathrm{2}\theta\right)=\mathrm{2}{sin}\left(\theta\right){cos}\left(\theta\right) \\ $$$$\:\:\:\:\:{note}:{sin}\left(\frac{\mathrm{2}{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)={sin}\left(\pi−\frac{\mathrm{2}{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)={sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\: \\ $$$$\vdots \\ $$$${sin}\left(\frac{\left({m}+\mathrm{1}\right)\pi}{\mathrm{2}{m}+\mathrm{1}}\right)={sin}\left(\pi−\frac{\left({m}+\mathrm{1}\right)\pi}{\mathrm{2}{m}+\mathrm{1}}\right)={sin}\left(\frac{{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$$\:\:{example}:\mid\mathrm{1}−{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{2}{m}+\mathrm{1}}} \mid=\mid\mathrm{1}−{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)−{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\mid \\ $$$$=\mid\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)−\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right){cos}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\mid \\ $$$$=\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\mid{sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)−{icos}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\mid=\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right) \\ $$$${from}\:\left(\ast\right)\:{and}\left(\:{notes}\right)=:: \\ $$$$\mathrm{2}^{\mathrm{2}{m}} \left({sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)…{sin}\left(\frac{{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)\right)^{\mathrm{2}} =\mathrm{2}{m}+\mathrm{1} \\ $$$$\:\:{sin}\left(\frac{\pi}{\mathrm{2}{m}+\mathrm{1}}\right)…{sin}\left(\frac{{m}\pi}{\mathrm{2}{m}+\mathrm{1}}\right)=\frac{\sqrt{\mathrm{2}{m}+\mathrm{1}}}{\mathrm{2}^{{m}} }\:\checkmark \\ $$$$ \\ $$$$\: \\ $$
Commented by MathSh last updated on 28/Dec/20
Thanks sir
$${Thanks}\:{sir} \\ $$
Commented by mnjuly1970 last updated on 28/Dec/20
you are welcome...
$${you}\:{are}\:{welcome}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *