Question Number 54730 by yorrick23ralph@gmail.com last updated on 09/Feb/19

$${prove}\:{lnx}\leqslant{x} \\ $$
Commented by Abdo msup. last updated on 09/Feb/19
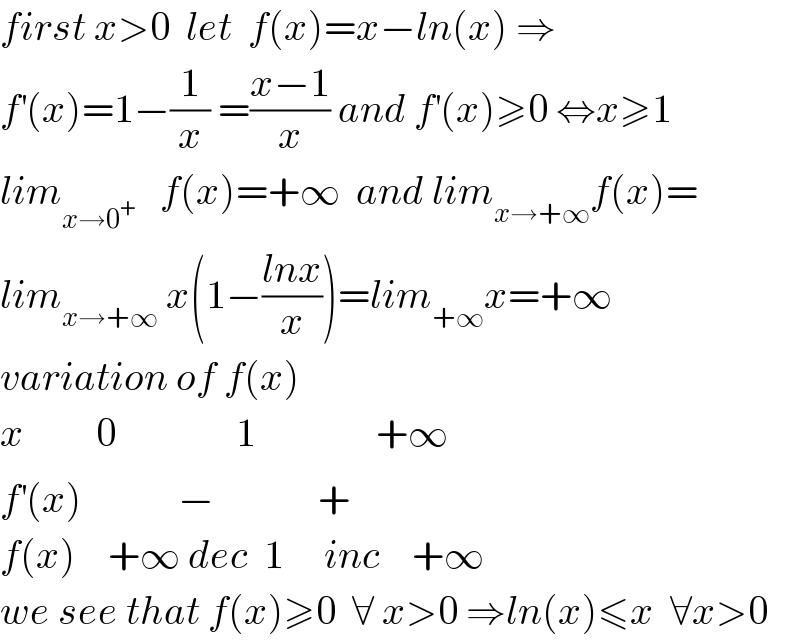
$${first}\:{x}>\mathrm{0}\:\:{let}\:\:{f}\left({x}\right)={x}−{ln}\left({x}\right)\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\mathrm{1}−\frac{\mathrm{1}}{{x}}\:=\frac{{x}−\mathrm{1}}{{x}}\:{and}\:{f}^{'} \left({x}\right)\geqslant\mathrm{0}\:\Leftrightarrow{x}\geqslant\mathrm{1} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:{f}\left({x}\right)=+\infty\:\:{and}\:{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)= \\ $$$${lim}_{{x}\rightarrow+\infty} \:{x}\left(\mathrm{1}−\frac{{lnx}}{{x}}\right)={lim}_{+\infty} {x}=+\infty \\ $$$${variation}\:{of}\:{f}\left({x}\right) \\ $$$${x}\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$${f}^{'} \left({x}\right)\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$$${f}\left({x}\right)\:\:\:\:+\infty\:{dec}\:\:\mathrm{1}\:\:\:\:\:{inc}\:\:\:\:+\infty \\ $$$${we}\:{see}\:{that}\:{f}\left({x}\right)\geqslant\mathrm{0}\:\:\forall\:{x}>\mathrm{0}\:\Rightarrow{ln}\left({x}\right)\leqslant{x}\:\:\forall{x}>\mathrm{0} \\ $$
Commented by yorrick23ralph@gmail.com last updated on 09/Feb/19

$${thanks}\:{sir} \\ $$
Commented by mr W last updated on 10/Feb/19
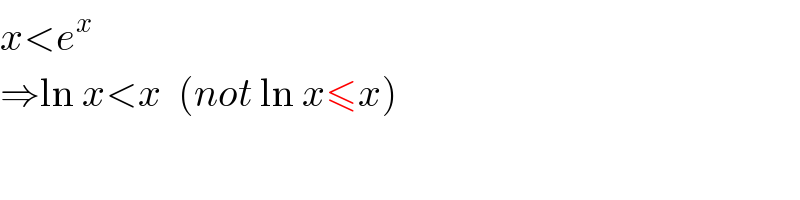
$${x}<{e}^{{x}} \\ $$$$\Rightarrow\mathrm{ln}\:{x}<{x}\:\:\left({not}\:\mathrm{ln}\:{x}\leqslant{x}\right) \\ $$
