Question Number 97956 by M±th+et+s last updated on 10/Jun/20
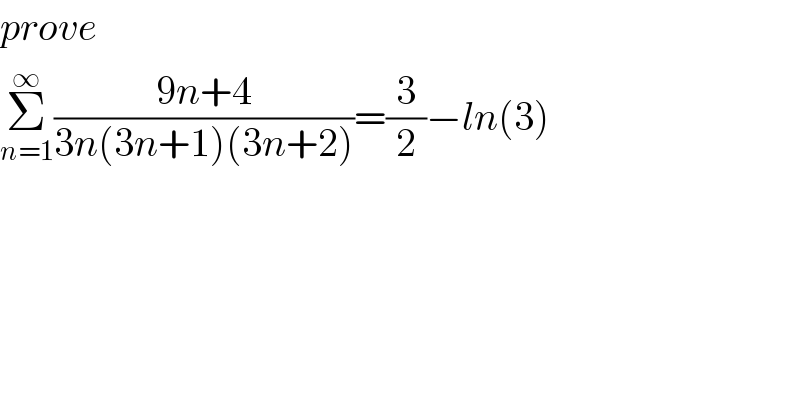
$${prove} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{9}{n}+\mathrm{4}}{\mathrm{3}{n}\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}=\frac{\mathrm{3}}{\mathrm{2}}−{ln}\left(\mathrm{3}\right) \\ $$
Answered by maths mind last updated on 13/Jun/20
![=Σ_(n≥1) ((4(3n+1)−3n)/(3n(3n+1)(3n+2))) =4Σ(1/(3n(3n+2)))−Σ(1/((3n+1)(3n+2))) =(4/9)Σ_(n≥1) (1/(n(n+(2/3))))−(1/9)Σ_(n≥1) (1/((n+(1/3))(n+(2/3)))) =(4/9)Σ_(n≥0) (1/((n+1)(n+(5/3))))−(1/9)Σ_(n≥0) (1/((n+(4/3))(n+(5/3)))) =(4/9).((Ψ((5/3))−Ψ(1))/((5/3)−1))−(1/9).((Ψ((5/3))−Ψ((4/3)))/((5/3)−(4/3))) S=(2/3)(Ψ((5/3))−Ψ(1))−(1/3)(Ψ((5/3))−Ψ((4/3))) (1/3)(Ψ((5/3))+Ψ((4/3)))−(2/3)Ψ(1) Ψ((p/q))=−γ−ln(2q)−(π/2)cot(((pπ)/q))+2Σ_(k=0) ^([((q−1)/2)]) cos(((2pπk)/q))ln(sin(((pkπ)/q))) Ψ((5/3))=(3/2)+Ψ((2/3)),Ψ((4/3))=3+Ψ((1/3)) Ψ((2/3))=−γ−ln(6)−(π/2)cot(((2π)/3))+2cos(((4π)/3))ln(sin(((2π)/3))) =−γ−ln(6)+(π/(2(√3)))−ln(((√3)/2)) Ψ((1/3))=−γ−ln(6)−(π/(2(√3)))−ln(((√3)/2)) S=(1/3)(−2γ−ln(27)+(3/2)+3)−(2/3)(−γ) S=ln((1/3))+(3/2)=(3/2)−ln(3)](https://www.tinkutara.com/question/Q98437.png)
$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{4}\left(\mathrm{3}{n}+\mathrm{1}\right)−\mathrm{3}{n}}{\mathrm{3}{n}\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)} \\ $$$$=\mathrm{4}\Sigma\frac{\mathrm{1}}{\mathrm{3}{n}\left(\mathrm{3}{n}+\mathrm{2}\right)}−\Sigma\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{9}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)}−\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{9}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\frac{\mathrm{5}}{\mathrm{3}}\right)}−\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{4}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{5}}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{9}}.\frac{\Psi\left(\frac{\mathrm{5}}{\mathrm{3}}\right)−\Psi\left(\mathrm{1}\right)}{\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{9}}.\frac{\Psi\left(\frac{\mathrm{5}}{\mathrm{3}}\right)−\Psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)}{\frac{\mathrm{5}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}} \\ $$$${S}=\frac{\mathrm{2}}{\mathrm{3}}\left(\Psi\left(\frac{\mathrm{5}}{\mathrm{3}}\right)−\Psi\left(\mathrm{1}\right)\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\Psi\left(\frac{\mathrm{5}}{\mathrm{3}}\right)−\Psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left(\Psi\left(\frac{\mathrm{5}}{\mathrm{3}}\right)+\Psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\right)−\frac{\mathrm{2}}{\mathrm{3}}\Psi\left(\mathrm{1}\right) \\ $$$$\Psi\left(\frac{{p}}{{q}}\right)=−\gamma−{ln}\left(\mathrm{2}{q}\right)−\frac{\pi}{\mathrm{2}}{cot}\left(\frac{{p}\pi}{{q}}\right)+\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\left[\frac{{q}−\mathrm{1}}{\mathrm{2}}\right]} {\sum}}{cos}\left(\frac{\mathrm{2}{p}\pi{k}}{{q}}\right){ln}\left({sin}\left(\frac{{pk}\pi}{{q}}\right)\right) \\ $$$$\Psi\left(\frac{\mathrm{5}}{\mathrm{3}}\right)=\frac{\mathrm{3}}{\mathrm{2}}+\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right),\Psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{3}+\Psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=−\gamma−{ln}\left(\mathrm{6}\right)−\frac{\pi}{\mathrm{2}}{cot}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\mathrm{2}{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{3}}\right){ln}\left({sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right) \\ $$$$=−\gamma−{ln}\left(\mathrm{6}\right)+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\Psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=−\gamma−{ln}\left(\mathrm{6}\right)−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{3}}\left(−\mathrm{2}\gamma−{ln}\left(\mathrm{27}\right)+\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\left(−\gamma\right) \\ $$$${S}={ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}−{ln}\left(\mathrm{3}\right) \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 13/Jun/20

$${well}\:{done}\:{prof}.{math}\:{mind}\:{you}\:{are} \\ $$$${intellignt} \\ $$
